Arbeitsblatt: Lineare Gleichungssysteme mit zwei Variablen

(zu Thema Mathematik 5 5, S. 88 - 91, zu BIFIE GK AG2.5)

  • Lernziele: Ein lineares Gleichungssystem mit zwei Variablen in Normalform anschreiben können, verschiedene Verfahren zielgerichtet anwenden können (Gleichsetzungsverfahen, Substitutionsmethode, Elminiationsverfahren) und grafische Methoden verwenden können.
  • Überblick, Recherche: Thema Mathematik 5 5, S. 84 - 85, Gleichungen
  • Hilfsmittel: Computer-Algebra-System, GeoGebra, „Zettel und Bleistift“

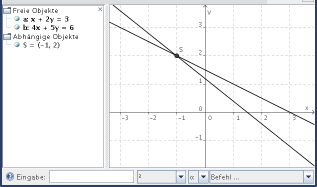Screenshot GeoGebraFasse die verschiedenen Lösungsverfahren an Hand des folgenden Beispiels zusammen: 

 x + 2y = 3
4x + 5y = 6

Aufgaben:

  1. 3x - 4y = 1, x + 2y = 7, Lösung: x = 3, y = 2
  2. 4x - 3y = 3, 3x + 4y = -4, Lösung: x = 0, y = -1
  3. 7x - 3y = 15, 2x + y = -5, Lösung: x = 0, y = -5
  4. 5x + 3y = -3, 5x - 4y = 4, Lösung: x = 0, y = -1

Forme zunächst in die Normalform um:

  1. tex:\frac {2x} 3 - \frac {4y} 5 = 4, tex:\frac {5x} 3 + \frac {3y} 4 = 10, Lösung: x = 6, y = 0
  2. tex:\frac {2x} 3 + \frac y 4 = -2, tex:\frac {4x} 3 + \frac {3y} 8 = 1, Lösung: x = 12, y = -40
  3. tex:- \frac {x} 8 + \frac {y} 5 = 1, tex:\frac {x} 7 - \frac {y} 5 = 1, Lösung: x = 112, y = 75
  4. tex:\frac {5x} 3 - \frac {3y}5 = 4, tex:\frac{2x} 3 - \frac y 5 = 0, Lösung: x = -12, y = -40

Gib an, bei welchen Eigenschaften der linearen Gleichungssysteme mit 2 Unbekannten (1) genau eine Lösung vorliegt, (2) keine Lösung vorliegt, (3) unendlich viele Lösungen vorliegen!

Zusammenfassung, Ausblick:


Zuletzt angesehen: • ab_gleichsys01