Zurück zu: 5.Klasse Vektoren Skalares Produkt

Geometrische Interpretation des skalaren Produkts zweier Vektoren

zu Thema Mathematik 5 5, S. 188 - 189, zu BIFIE GK AG3.3

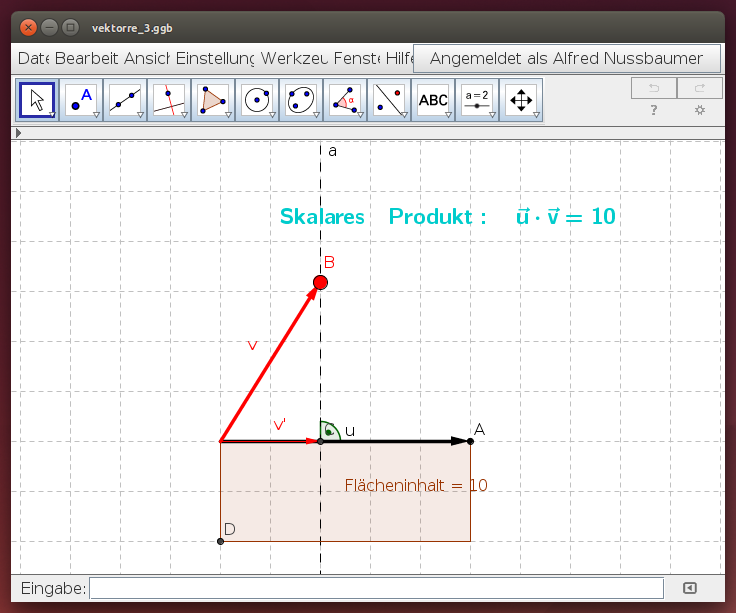
Für Vektoren im zweidimensionalen und dreidimensionalen Raum können wir das skalare Produkt tex:\vec a \cdot \vec b geometrisch veranschaulichen: Multipliziere die Länge des ersten Vektors mit der Länge der Normalprojektion des zweiten Vektors auf den ersten. Das Ergebnis entspricht dem Flächeninhalt eines Rechtecks, dessen Seitenlängen dem Betrag des ersten Vektors und dem Betrag der Normalprojektion des zweiten Vektors auf den ersten entsprechen.

Sieh dir diesen kompliziert klingenden Sachverhalt mit dem folgenden GeoGebra-Arbeitsblatt an. Verschiebe den zweiten Vektor, indem du seine Spitze B in verschiedene Positionen ziehst:

Screenshot: Alfred Nussbaumer

Download der GeoGebra-Datei

Aufgaben:

  1. Der Flächeninhalt des Rechtecks ist immer positiv. Unter welchen Voraussetzungen ist das skalare Produkt der beiden Vektoren positiv und wann ist es negativ?
  2. Verschiebe die Spitze B des zweiten Vektors horizontal: Wie wirkt sich das auf das skalare Produkt aus?
  3. Verschiebe die Spitze B des zweiten Vektors vertikal: Wie wirkt sich das auf das skalare Produkt aus?
  4. Untersuche - mit vielen verschiedenen Positionen des zweiten Vektors -, unter welchen Voraussetzungen das skalare Produkt der beiden Vektoren null ist!

Zurück zu Vektorrechnung


Zuletzt angesehen: • homogene_lineare_funktion • wahrscheinlichkeitsrechner • inhomogene_lineare_funktion • komplexe_zahlen • skalares_produkt_geometrisch