Entwicklung einer Fischpopulation
Der Populationszuwachs in einem Fischteich ist proportional zur Anzahl der vorhandenen Fische (vgl. exponentielles Modell) und proportional zum Freiraum (vgl. beschränktes Modell). Das logistische Modell kombiniert offensichtlich das exponentielle Modell und beschränkte Modell.
Beispiel: Fischpopulation (logistisches Wachstum)
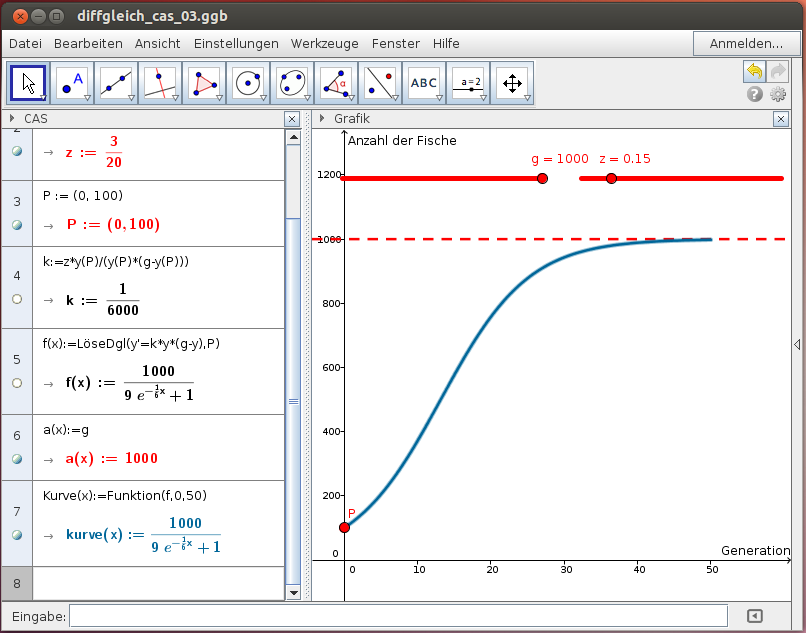
Zu Beginn sind es 100 Fische, im ersten Jahr kommt es zu einem Zuwachs von 15 %. Der Lebensraum ist auf 1000 Fische beschränkt. Beschreibe die Entwicklung der Fischpopulation durch ein logistisches Modell!
Der Fischzuwachs ist proportional zur Anzahl der Fische
und zum Freiraum
:
Differenzengleichung:
Dabei ist der Bestand nach
Iterationen. Den Faktor
berechnen wir aus dem Zuwachs bei der ersten Iteration:
Durch Grenzübergang erhalten wir die Differentialgleichung:
. Wir lösen die Differentialgleichung exakt in der CAS-Ansicht:
Aufgaben:
- Vergleiche mit dem diskreten Modell zur Entwicklung der Fischpopulation!
- Untersuche, wie die Lösung von den Ausgangswerten (Anfangsbestand P, Grenzwert g, Zuwachs z) abhängt!
- Vergleiche die Lösung mit der numerischen Lösung in der Algebra-Ansicht (Fischpopulation)!
Zurück zu Dynamische Systeme