Temperaturausgleich

8 S.130 - 131

Um von einem diskreten Modell zu einem kontinuierlichen Modell zu gelangen, wird die Differenzengleichung mittels Grenzwert für $tex:\Delta t \rightarrow 0$ in eine Differenzialgleichung umgewandelt.

Beispiel: Abkühlkurve (beschränktes Wachstum)

80°C heißes Wasser kühlt bei einer Raumtemperatur von 20°C während eines Zeitraumes von 60 Minuten ab. Bestimme die Abkühlkurve!

Differenzengleichung:

$tex:\Delta y = 0,03 \cdot (20 - y_n)$ mit tex:y_0 = 80

Differentialgleichung:

$tex:y'(t) = 0,03 \cdot (20 - y)$ mit tex:y_0 = 80

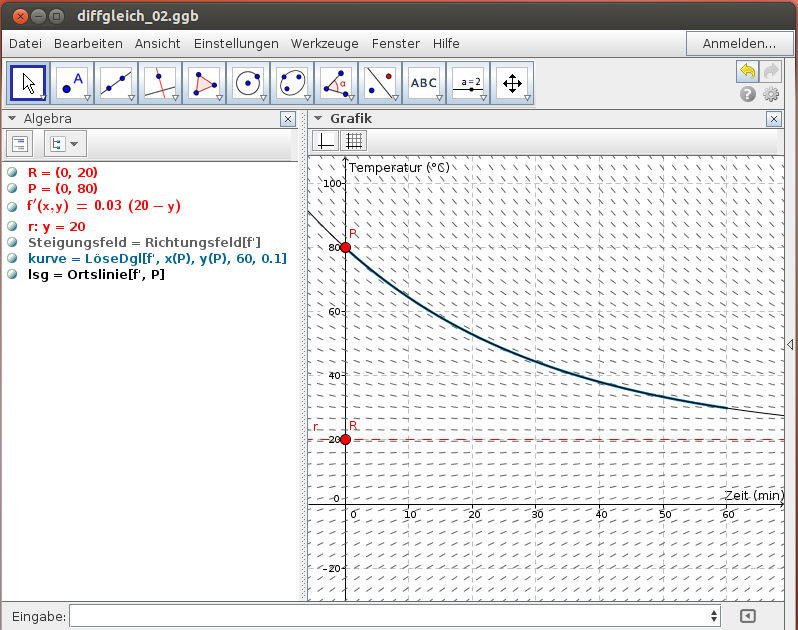
Wir lösen die Differentialgleichung numerisch in der Algebra-Ansicht:

Die Differentialgleichung wird als Funktion f'(x,y) in den beiden Variablen x und y eingegeben.
Der Befehl Richtungsfeld(f') gibt das Steigungsfeld zur angegebenen Differentialgleichung im Grafikfenster aus.
Der Befehl LöseDgl(<f'(x,y)>,<Startwert x>,<Startwert y>, <Ende>, <Schrittweite> gibt eine numerische Lösung im Grafikfenster aus.
Allenfalls kann die allgemeine Lösung der Differentialgleichung als Ortslinie mit dem Befehl Ortslinie(<f'>,<Anfangswert>) ausgegeben werden.

Download der GeoGebra-Datei

Aufgaben:

Vergleiche mit dem diskreten Modell zum Temperaturausgleich!
Untersuche, wie die Lösung vom Ausgangswert P (Ausgangstemperatur) und von der Raumtemperatur r abhängt!
Vergleiche mit der exakten Lösung in der CAS-Ansicht (Temperaturausgleich)!

Zurück zu Dynamische Modelle

Zuletzt angesehen: • temperaturausgleich_1

Suche