Temperaturausgleich
 6, S. 176 - 177, 8, S. 128 - 129
6, S. 176 - 177, 8, S. 128 - 129
Hat ein Objekt eine andere Temperatur als die Umgebung („Raumtemperatur“), dann gleicht sich die Temperatur nach einer gewissen Zeit aus: Eine heiße Flüssigkeit kühlt aus, ein kalter Körper erwärmt sich bis zur Raumtemperatur …
Es liegt ein beschränktes Wachstumsmodell vor. Wir lösen es hier mit einem diskreten Modell.
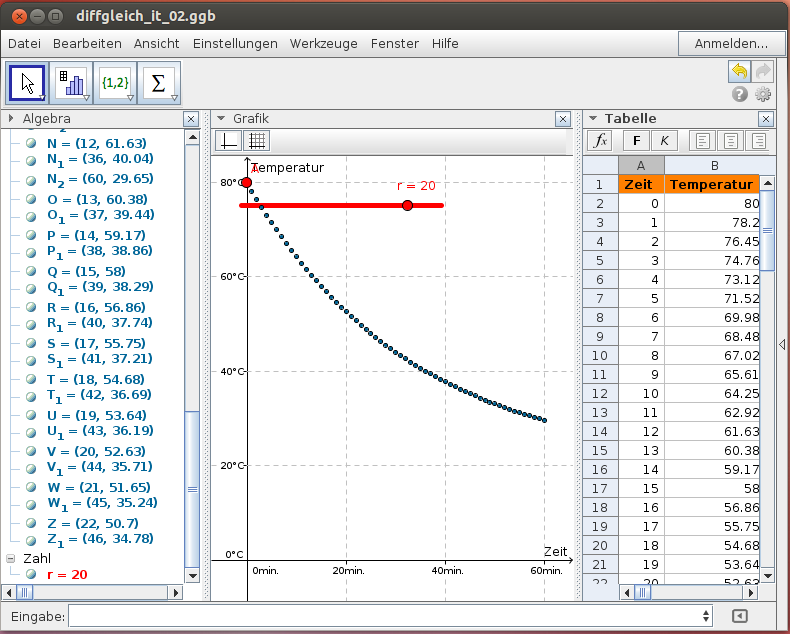
Beispiel:
80°C heißes Wasser kühlt bei einer Raumtemperatur von 20°C während eines Zeitraumes von 60 Minuten ab. Bestimme die Abkühlkurve!
mit
Wir berechnen die Temperaturwerte iterativ in der Tabellenansicht:
Hinweis: Gib die Iterationsformel als Berechnungsformel in das Tabellenfeld B3 ein: =B2 + 0.03 (r - B2) und kopiere diese in die nächsten Felder!
Aufgaben:
- Wähle verschiedene Ausgangstemperaturen, indem du den roten Punkt A verschiebst und interpretiere die Ergebnisse, wenn die Ausgangstemperatur oberhalb oder unterhalb der Raumtempertur r liegt!
- Wir erhalten aus obiger Iterationsgleichung die folgende Differenzengleichung:
mit
,
mit
. Rechne nach!