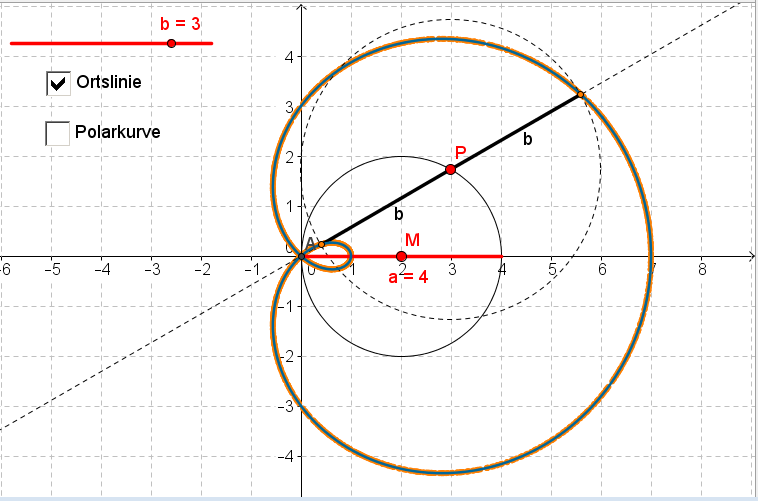
Die Pascalsche Schnecke als Spezialfall der Konchoide
7, Themenheft GeoGebra
Die Pascalsche Schnecke ist ein Spezialfall der Konchoide: Während die Konchoide mit Hilfe einer Leitgeraden erhalten werden kann, erhält man die Pascalsche Schnecke mit Hilfe eines Leitkreises:
Aufgaben:
- Bilde die Punktespur, indem du den Punkt P auf dem Leitkreis verschiebst!
- Vergleiche die Punktespur mit der Ortslinie!
- Gib die Gleichung der zu den Werten von a und b passenden Polarkurve ein und vergleiche ihren Graphen mit der Ortslinie und mit der Punktespur!
- Variiere a, indem du den Punkt A auf der x-Achse verschiebst (a ist der Durchmesser des Leitkreises)!
- Variiere b mit dem Schieberegler!
- Argumentiere, wie die Form der Pascalschen Schnecke von den Werten für a und b abhängt (vergleiche dies mit Pascalsche Schnecke)!
Zurück zu Parametrisierte Kurven
