Inhaltsverzeichnis
Thema: Lineare Optimierung
6 S. 48 - 49
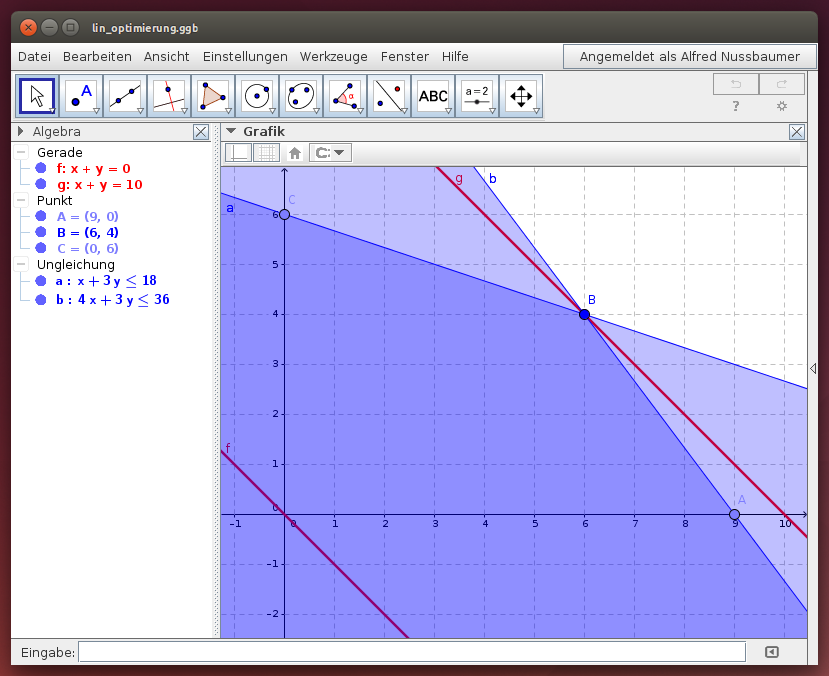
Wir betrachten lineare Optimierungsaufgaben mit zwei Unbekannten x und y. In diesem Fall erhalten wir aus einem System von linearen Ungleichungen ein Polygon. An einer der Ecken des Polygons finden wir die optimale Lösung. Die Bedingungen und
legen fest, dass keine negativen Lösungen möglich sind („Nichtnegativitätsbedingungen“).
Aufgabe:
Gib im folgenden GeoGebra-Applet zwei lineare Ungleichungen a und b in den Variablen x und y und die Lösungsfunktion f(x,y) ein und bestimme die Lösung durch Parallelverschieben!
Hinweis: Gib die Ungleichungen und die Lösungsfunktion über die Eigenschaften der Objekte in der Algebra-Ansicht ein.
Ausblick
- Vergleiche mit
- Themenheft Angewandte Mathematik (7. Klasse), S. 4 - 9! - Erweitere das obige GeoGebra-Applet um eine weitere Ungleichung c!
Studium
- Mathematik
- Wirtschaftswissenschaften
Zurück zu 6. Klasse
