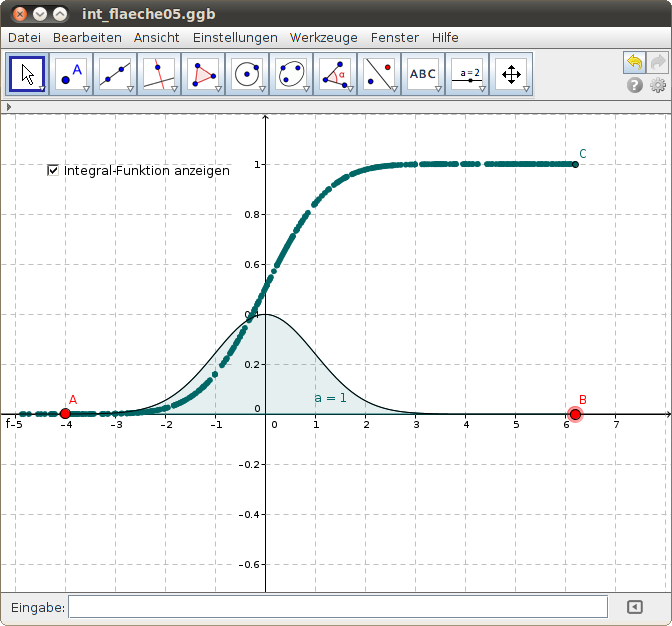
Der Flächeninhalt unter der Gauß'schen Glockenkurve
Die Funktion beschreibt die Standard-Normalverteilung. Wähle beliebige Intervalle [x(A), x(B)] im folgenden GeoGebra-Modell aus, indem du die roten Punkte A und B verschiebst und lies den Wert der zugehörigen Fläche unter der Kurve ab:
Aufgaben:
- Stelle die linke Grenze des Intervalls (den roten Punkt A) auf x = - 4 und zeige die Integralfunktion an! Beschreibe ihre Eigenschaften!
- Stelle die linke Grenze des Intervalls (den roten Punkt A) auf x = 0 und zeige die Integralfunktion an!
Zurück zu Flächeninhalt unter einer Kurve | Anwendungen der Integralrechnung