Inhaltsverzeichnis
Wahrscheinlichkeitsrechnung
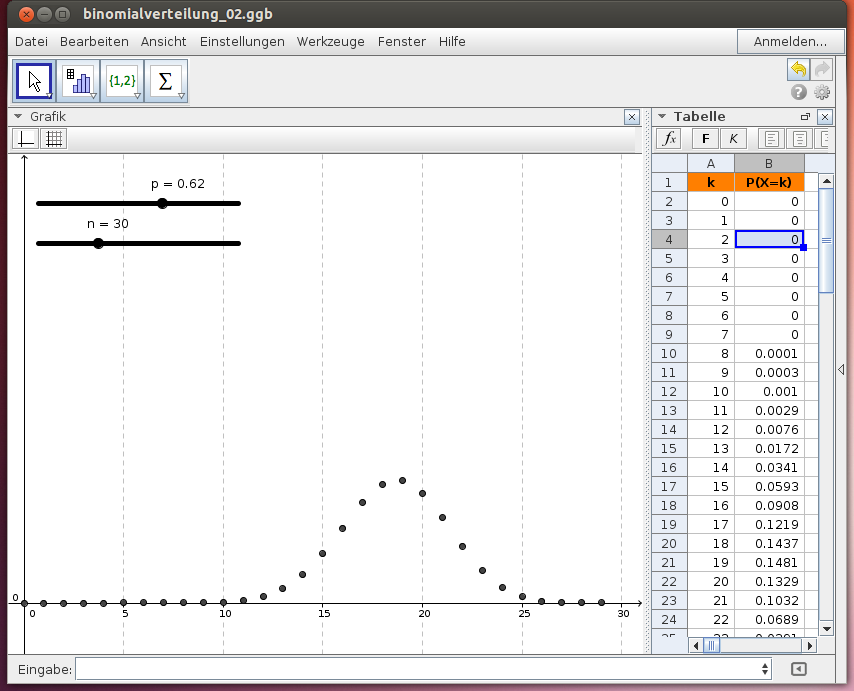
Binomialverteilung
Der Befehl Binomialkoeffizient(n,k) berechnet .
Der Befehl Binomial(<Anzahl der Versuche>, <Erfolgswahrscheinlichkeit>, <Anzahl der Erfolge>, <Wahrheitswert>) liefert die Binomialverteilung. Dabei ist
n ... Anzahl der Versuche p ... Wahrscheinlichkeit k ... Anzahl der Erfolge ''false'' ... P(X = k) und ''true'' für P(X ≤ k)
Im folgenden GeoGebra-Beispiel steht in der Zelle B4 der Befehl =Binomial(n, p, A4, false):
Aufgaben:
- Variiere im obigen Beispiel die Wahrscheinlichkeit p mit dem Schieberegler und interpretiere das Diagramm!
- Variiere im obigen Beispiel die Anzahl n der Versuche mit dem Schieberegler und interpretiere das Diagramm!
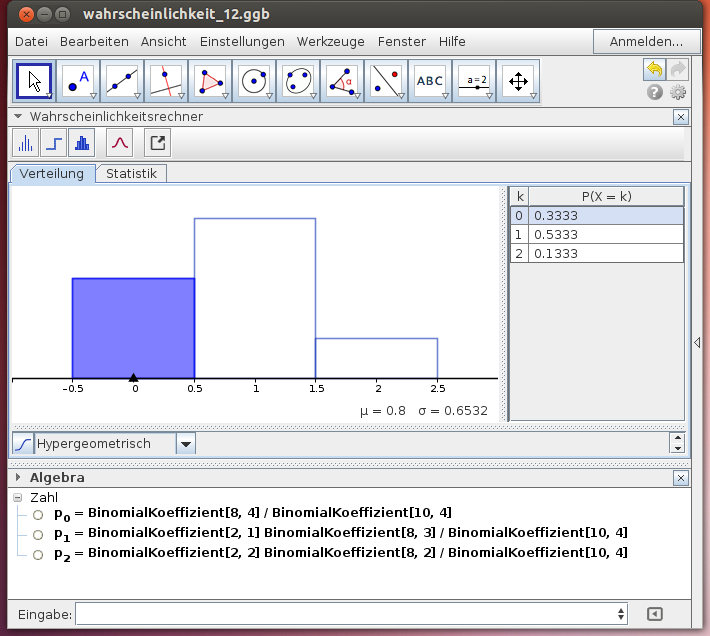
Hypergeometrische Verteilung
Beim Ziehen einer Stichprobe ohne Zurücklegen ändert sich die Wahrscheinlichkeit - wir rechnen mit der hypergeometrischen Verteilung. Im folgenden GeoGebra-Beispiel werden aus 10 Eiern, von denen 2 Eier nicht in Ordnung sind, 4 Eier für eine Speise entnommen:
Aufgaben:
- Rechne die Wahrscheinlichkeitswerte der Tabelle nach und begründe die Rechenvorschrift!
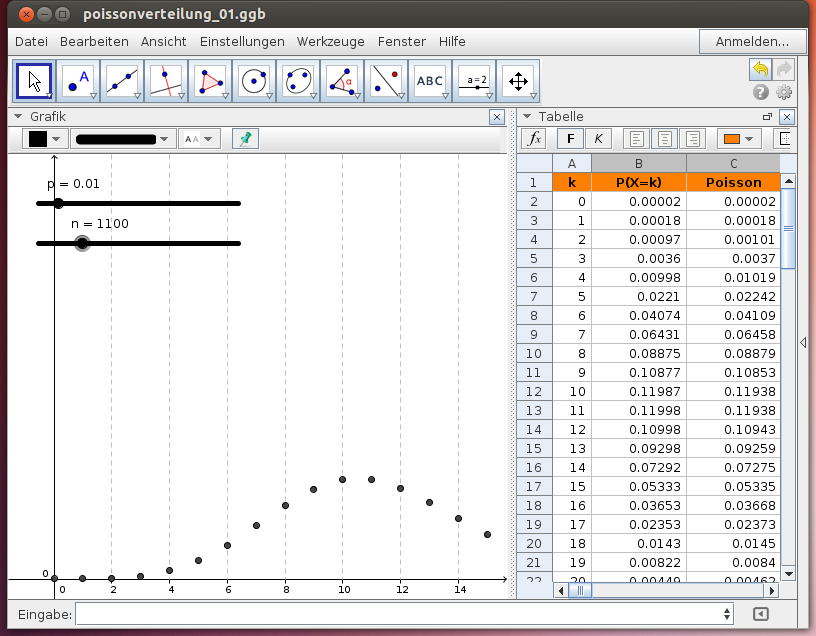
Poissonverteilung
Für kleine Wahrscheinlichkeiten p und große Stichprobenumfänge n kann die Binomialverteilung durch die Poissonverteilung approximiert werden:
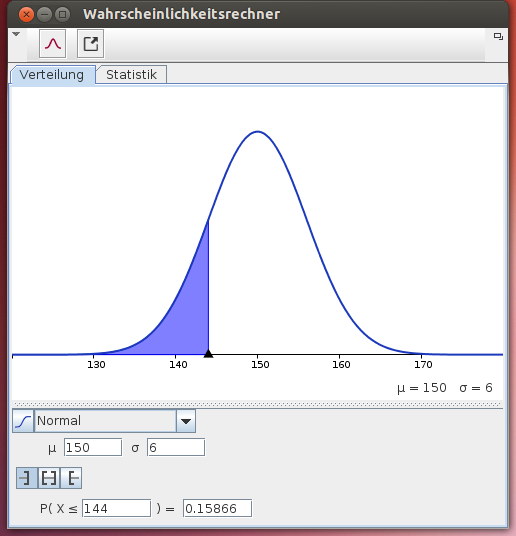
Normalverteilung
Der Befehl Normal(<Erwartungswert>, <Standardabweichung>, x) liefert den Wert für P(X<x); z.B. Normal(150,6,144) = 0.15866…
Vergleiche:
Beachte: Bei vielen Aufgabenstellungen ist es sinnvoll mit dem Wahrscheinlichkeitsrechner zu arbeien.
Zurück zu Themenheft Arbeiten mit GeoGebra 7 - 8 | Stochastik | Inhaltsbereich Wahrscheinlichkeit und Statistik