Hypergeometrische Verteilung

tm.jpg 7, S. 22 - 23

Beim Ziehen einer Stichprobe ohne Zurücklegen ändert sich die Wahrscheinlichkeit - wir rechnen mit der hypergeometrischen Verteilung anstelle der Binomialverteilung.

Aufgabe:

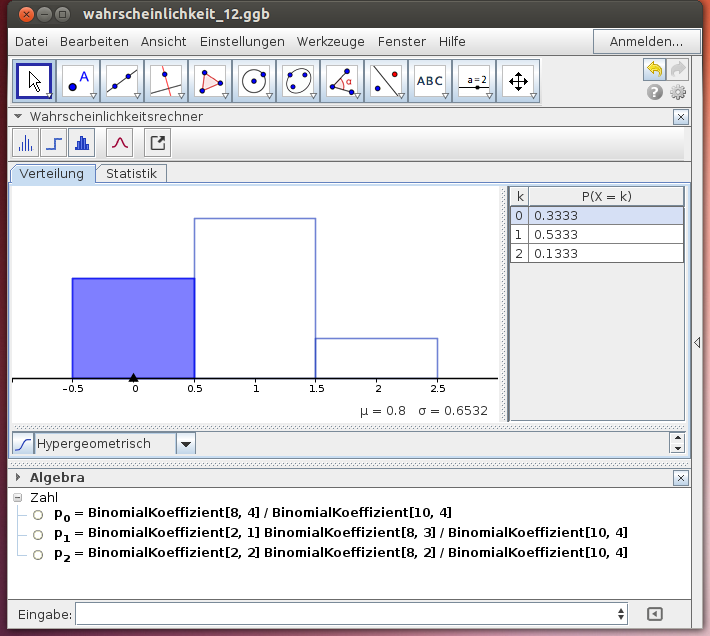
In einem Kühlschrank befinden sich 10 Eier, davon sind 8 in Ordnung. Jemand entnimmt 4 Stück für eine Speise. Die Zufallsvariable X gibt an, wie viele der entnommenen Eier nicht in Ordnung sind. Bestimme die Werte der Wahrscheinlichkeitsfunktion!

Screenshot: Alfred Nussbaumer

Ausblick:

Die hypergeometrische Verteilung hängt somit von drei Parametern ab:

  • N … Anzahl der Elemente der Grundgesamtheit
  • M … Anzahl der Elemente der Grundgesamtheit mit einer bestimmten Eigenschaft
  • n … Stichprobenumfang

Dann ist die Wahrscheinlichkeit, dass k Elemente mit der bestimmten Eigenschaft in der Stichprobe von n Elementen vorkommen, gegeben durch:

tex:P(X = k) = \frac {{M \choose k} {{N-M} \choose {n-k}}} {{N \choose n}}

  • Überprüfe die Gültigkeit dieser Formel am obigen Beispiel!

Zurück zu Stochastik


Zuletzt angesehen: • wahrscheinlichkeit_12