Diffie-Hellman Schlüsseltausch
Das Verfahren dient dazu, beiden Kommunikationspartnern auf sicherem Weg einen gemeinsamen Schlüssel S zur Verfügung zu stellen.
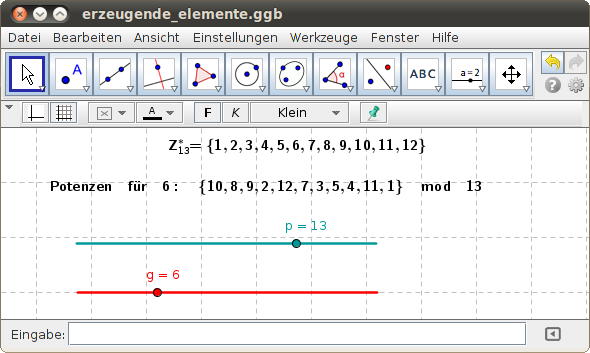
Die Grundlage bilden eine (große) Primzahl p und eine Basis g, der eine Restklasse mit möglichst großer Zykluslänge beschreibt. Weiters ermitteln die beiden Kommunikationspartner A (Alice) und B (Bob) jeweils Zufallszahlen a und b die kleiner als p - 1 sind. Die Zahl a steht nur Alice zur Verfügung, b ist nur Bob zur Verfügung.
Als erstes bestimmt Alice den Ausdruck mod p und übermittelt
an Partner Bob.
Partner Bob bestimmt den Ausdruck mod p und übermittelt
an Alice.
Mit den bekannten Parametern p und g können nun beide Partner folgende Ausdrücke berechnen:
Alice berechnet mit den Ausdruck
(Alice ist ja im Besitz der Geheimzahl a); Bob berechnet mit
den Ausdruck
(Bob besitzt ja b). Beide erhalten wegen der Kommutativität der (diskreten) Potenzierung den gleichen Wert, den sie als Schlüssel verwenden:
mod p bzw.
mod p.
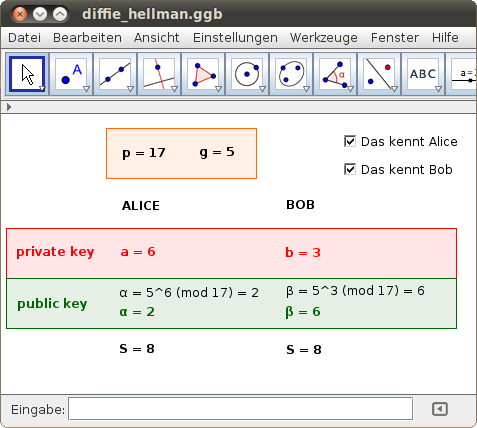
Gib im folgenden GeoGebra-Beispiel die Primzahl p, das erzeugende Element g und die beiden (zufällig gewählten) Zahlen a und b in der Eingabezeile ein. Die privaten und öffentlichen Schlüsselteile sowie der zur Verfügung stehende gemeinsame Schlüssel S werden umgehend berechnet. Wähle mit den Kontrollkästchen aus, welche Informationen angezeigt werden sollen!
Die Frage ist nur: Ist der auf diese Weise berechnet Schlüssel sicher - d.h. kann ihn ein Angreifer mit den bekannten Informationen (p,g, ,
) berechnen?
Zurück zu Lernpfad Kryptographie | GeoGebra 3.2: Texte codieren, Listen bearbeiten, Restklassenarithmetik ...