Inhaltsverzeichnis
Eine Funktion in kartesischen Koordinaten und in Polarkoordinaten darstellen
Aus dem kartesischen Graph einer Funktion lässt sich eine Polardarsellung
ableiten, indem die x-Koordinate als Drehwinkel
und die y-Koordinate als Abstand r vom Koordinatenursprung interpretiert wird.
In den folgenden GeoGebra-Applets wird sowohl der kartesische Graph als auch die zugehörige Polardarstellung an verschiedenen, grundlegenden Funktionen gezeigt.
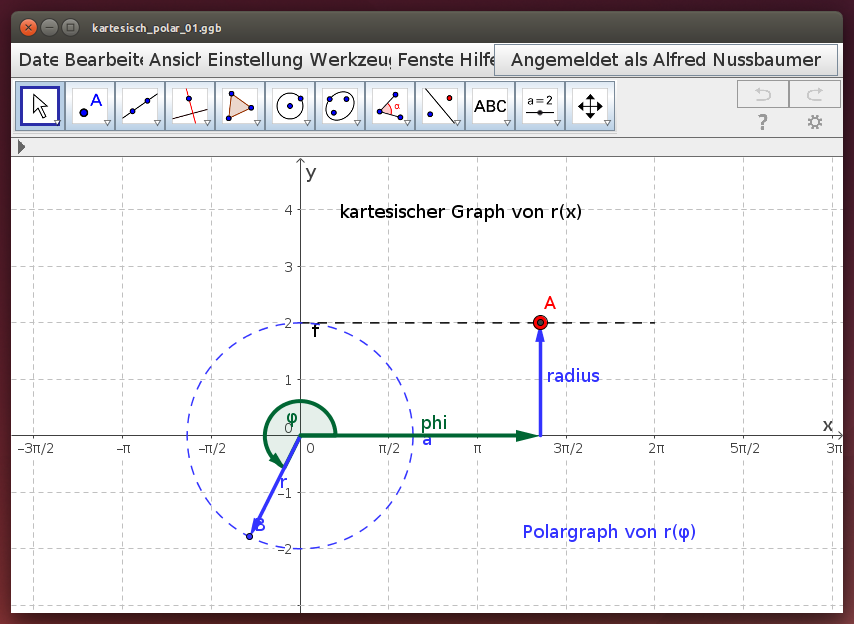
Konstante Funktion / Kreis
Untersuche die Polardarstellung der konstanten Funktion r(x) = 2. Verschiebe dazu im folgenden Geogebra-Datei den roten Punkt A auf dem kartesischen Graph und beobachte die Spur des blauen Punktes B auf dem Polargraph:
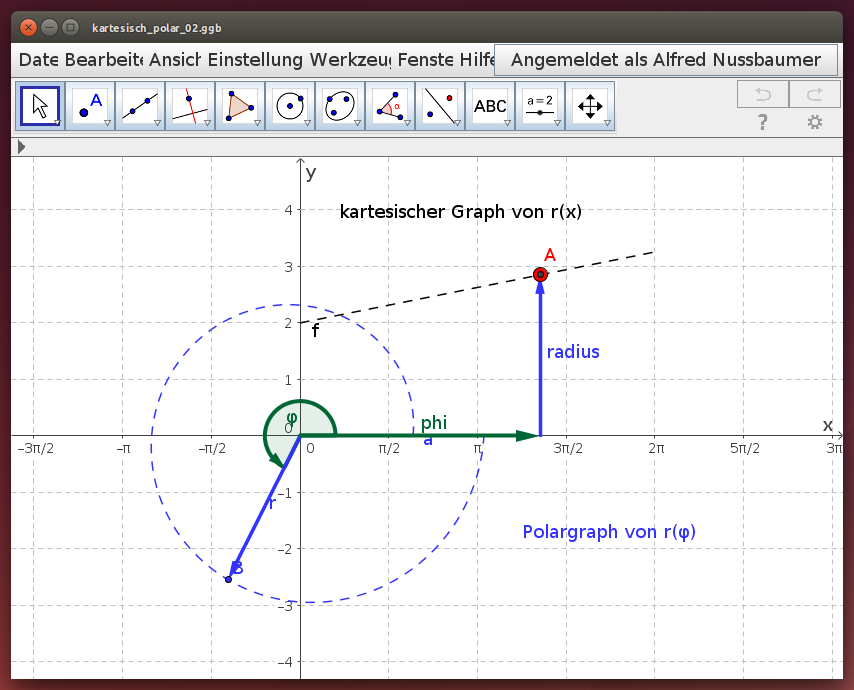
Lineare Funktion / Spirale
Untersuche die Polardarstellung der linearen Funktion r(x) = 2 + 0,2 x. Verschiebe dazu im folgenden Geogebra-Beispiel den roten Punkt A auf dem kartesischen Graph und beobachte die Spur des blauen Punktes B auf dem Polargraph:
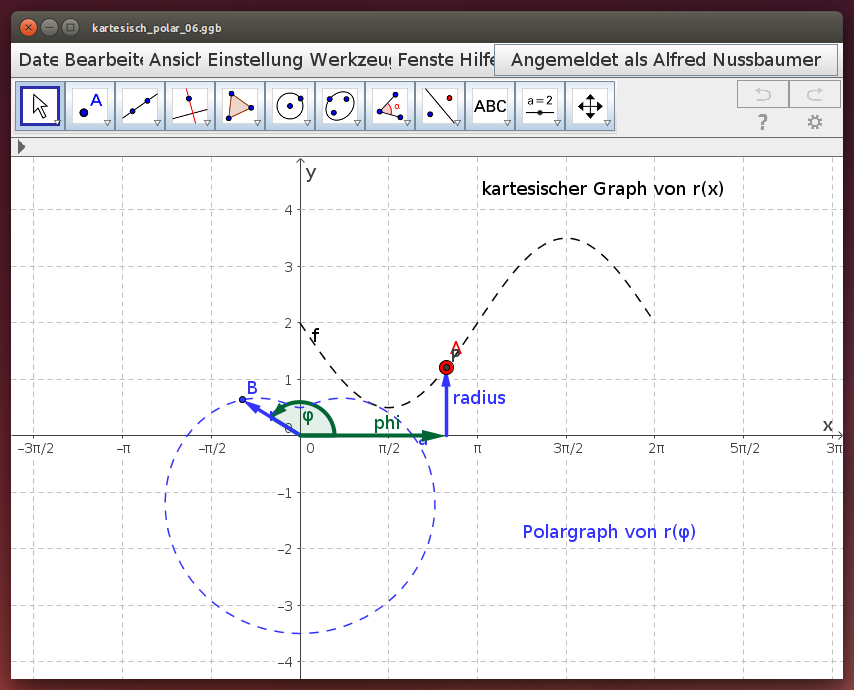
Sinusfunktion / Herzkurve
Untersuche die Polardarstellung der Sinusfunktion r(x) = 2 - 1,5 sin(x/2). Verschiebe dazu im folgenden Geogebra-Beispiel den roten Punkt A auf dem kartesischen Graph und beobachte die Spur des blauen Punktes B auf dem Polargraph:
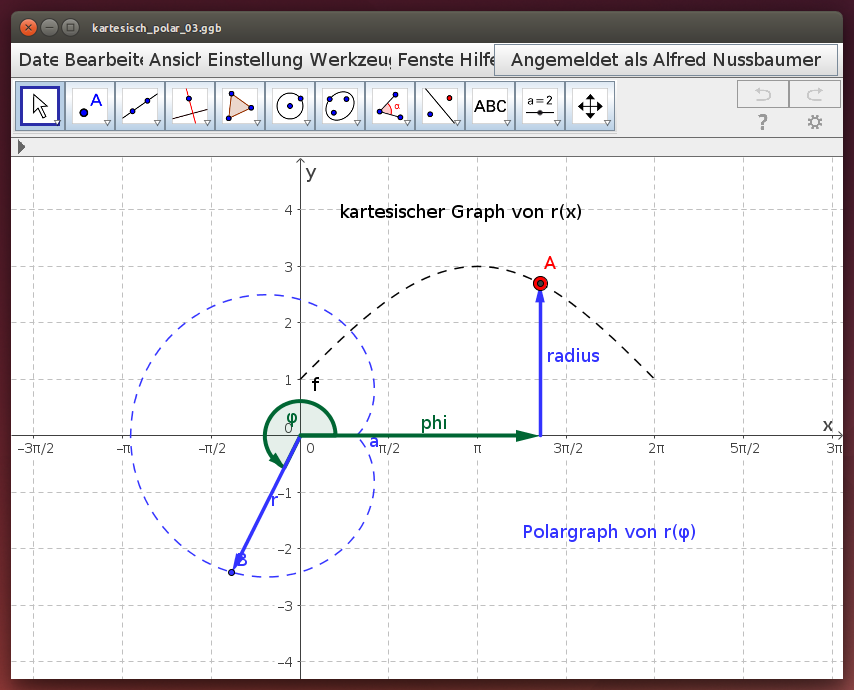
Sinusfunktion / Herzkurve
Untersuche die Polardarstellung der Sinusfunktion r(x) = 1 + 2 sin(x/2). Verschiebe dazu im folgenden Geogebra-Beispiel den roten Punkt A auf dem kartesischen Graph und beobachte die Spur des blauen Punktes B auf dem Polargraph:
Beschreibe den Unterschied zur oben dargestellten Herzkurve!
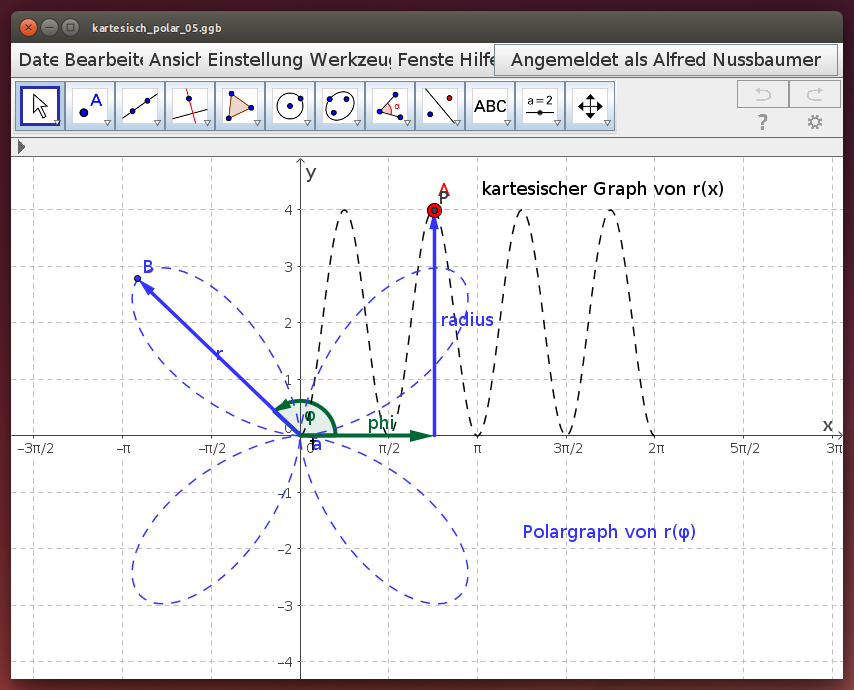
Cosinusfunktion / Rosette
Untersuche die Polardarstellung der Cosinusfunktion r(x) = 2 - 2 cos(4x). Verschiebe dazu im folgenden Geogebra-Beispiel den roten Punkt A auf dem kartesischen Graph und beobachte die Spur des blauen Punktes B auf dem Polargraph:
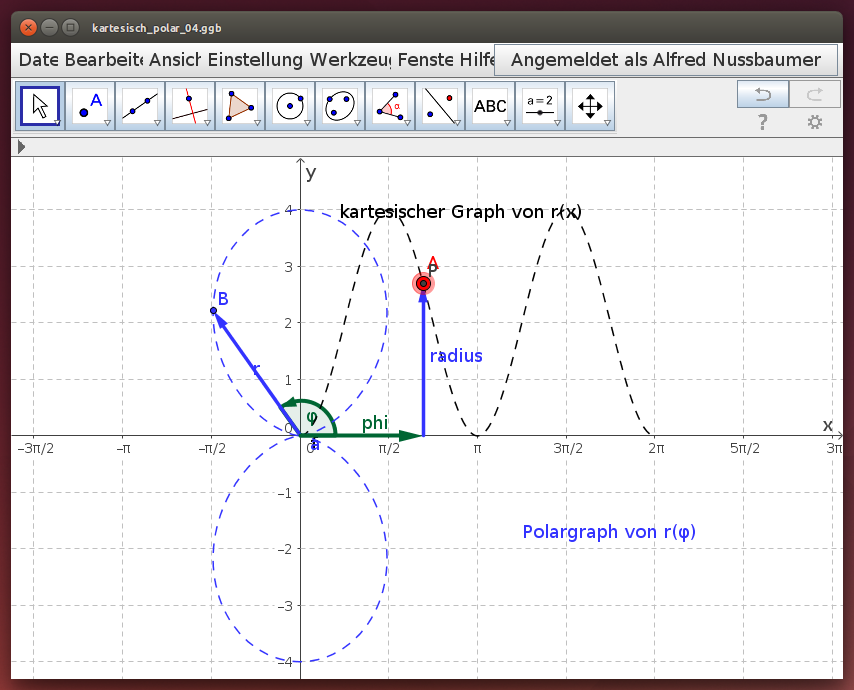
Cosinusfunktion / Lemniskate
Untersuche die Polardarstellung der Cosinusfunktion r(x) = 2 - 2 cos(2x). Verschiebe dazu im folgenden Geogebra-Beispiel den roten Punkt A auf dem kartesischen Graph und beobachte die Spur des blauen Punktes B auf dem Polargraph:
Beschreibe den Unterschied zur oben dargestellten Rosettenkurve!
Lies im Online-Lexikon nach: WikiPedia: Lemniskate
Aufgaben:
- Beschreibe, wie die Eigenschaften einer Funktion aus der kartesischen Darstellung abgelesen werden können!
- Beschreibe, wie die Eigenschaften einer Funktion aus der Polardarstellung abgelesen werden können!
- Erläutere, für welche Funktionen sich die Polardarstellung besonders gut eignen könnte!
- Lies und bearbeite den Artikel zu parametrisierten Kurven!
Siehe auch: Polarkoordinaten, Polardarstellung