elgamal

Elgamal

(zu )

Mit dem Elgamal-Algorithmus können Nachrichten verschlüsselt (und wieder entschlüsselt) und Nachrichten signiert werden.

Das Verfahren von Elgamal hat viele Gemeinsamkeiten mit dem Algorithmus von Diffie-Hellman:

Die Grundlage bilden eine (große) Primzahl p und eine Basis g, die eine Restklasse mit möglichst großer Zykluslänge beschreibt. Zu diesem Paar (p, g) bestimmen die Kommunikationspartner, Alice und Bob, zu ihren jeweils geheimen Schlüsseln a und b die öffentlichen Schlüsselteile α und β. Mit ihnen wird nun die Nachricht N verschlüsselt.

Bob verfährt folgendermaßen:

$tex:V = N \cdot \alpha^b$ (mod p) - Bob ist ja im Besitz des öffentlichen Schlüssels α von Alice.

Alice kann die verschlüsselte Nachricht V mit den nur ihr bekannten Schlüsseln entschlüsseln:

$tex:E = V \cdot \beta^{p - 1 - a}$ (mod p).

Wir müssen jetzt zeigen, dass $tex:E \equiv N$ (mod p) gilt - alle Rechnungen (mod p):

Wir setzen für V ein und erhalten:

$tex:E = (N \cdot \alpha^b) \cdot \beta^{p-1-a}$

Auf der Basis von g und p konnten die öffentlichen Schlüssel α und β bestimmt werden. Damit erhalten wir:

$tex:E = (N \cdot (g^a)^b) \cdot (g^b)^{p-1-a}$

Wir formen um und vereinfachen:

$tex:E = N \cdot (g^a)^b) \cdot (g^b)^{-a} \cdot g^{b \cdot (p - 1)}$

Damit erhalten wir:

$tex:E = N \cdot (g^{p-1})^b$

Mit Hilfe des Kleinen Satzes von Fermat, $tex:x^{p-1} \equiv 1$ (mod p) (vgl. Abschnitt Primzahlen) erhalten wir für die letzte Gleichung, da tex:g < p gilt:

$tex:E \equiv N \cdot 1^b \Rightarrow E \equiv N$ (mod p)

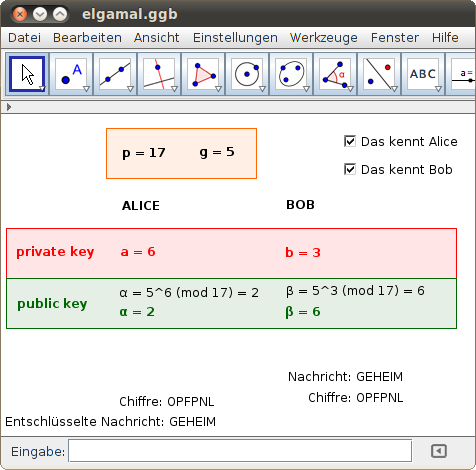
Wähle im folgenden GeoGebra-Beispiel die Primzahl p und den Modul g, sowie die beiden (geheimen) Zufallszahlen a und b. Bob will eine Nachricht verschlüsselt an Alice senden. Weise diesen Text der Variablen „Nachricht“ in der Eingabezeile zu:

Download der GeoGebra-Datei

Aufgaben:

Die Primzahl p kann im obigen GeoGebra-Beispiel höchstens den Wert 17 annehmen. Welche Konsequenzen hat das für die Klartextbuchstaben?
Begründe: Nur Nachrichten in Großbuchstaben werden im obigen GeoGebra-Beispiel richtig chiffriert und dechiffriert.
Wähle verschiedene Werte für p,g,a und b und beobachte die Auswirkungen auf die öffentlichen Schlüssel α und β. Wird dadurch der verschlüsselte Text beeinflusst?
Begründe: Der Schlüssel α = 1 oder β = 1 ist de facto unbrauchbar.
Untersuche, ob gleiche Buchstaben des Klartextes auch in der verschlüsselten Nachricht als gleiche Buchstaben aufscheinen. Welche Auswirkungen hat dies auf die Sicherheit des Verfahrens?
Technologie: Erweitere obiges GeoGebra-Modell auf einen größeren Zahlenbereich!

Zurück zu Lernpfad Kryptographie | GeoGebra 3.2: Texte codieren, Listen bearbeiten, Restklassenarithmetik ...