Tangente mittels Berührbedingung
Beispiel:
Bestimmte die Gleichung der Tangente und den Berührpunkt jener Tangente an die Parabel , die die Steigung
hat!
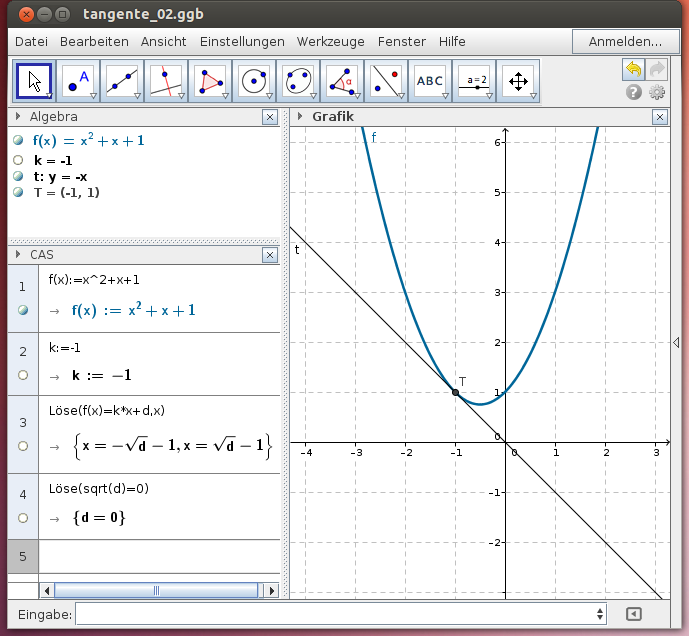
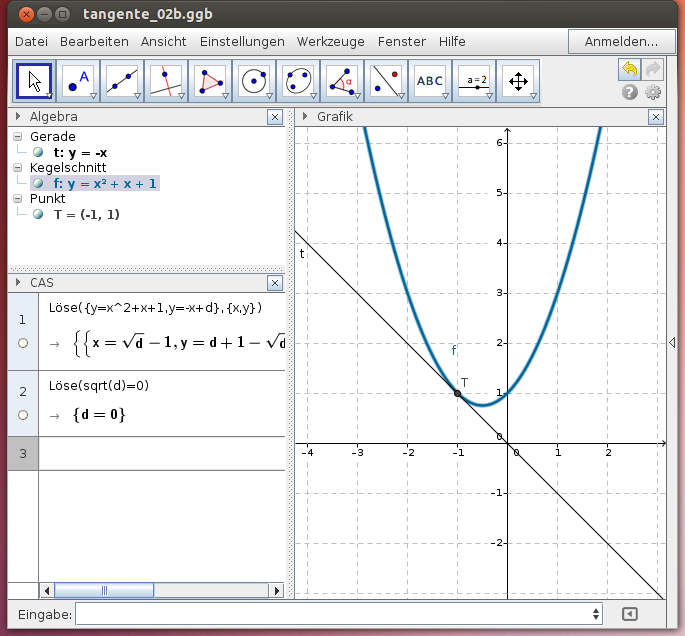
Lösung: Die Tangente hat die Gleichung y = -x + d. Bestimme „die Schnittpunkte“ der Parabel mit der Tangente. Da ein Berührpunkt vorliegt, ist die Diskriminante für die Lösung in x gleich Null - wir erhalten den Wert für d und somit die Geradengleichung für die Tangente:
Ergebnis: ,
.
Aufgaben:
- Löse ähnliche Aufgaben, z.B.: k = 2, p: y = 7x2 - 5x + 1
Zurück zu Grundlagen der Differentialrechnung