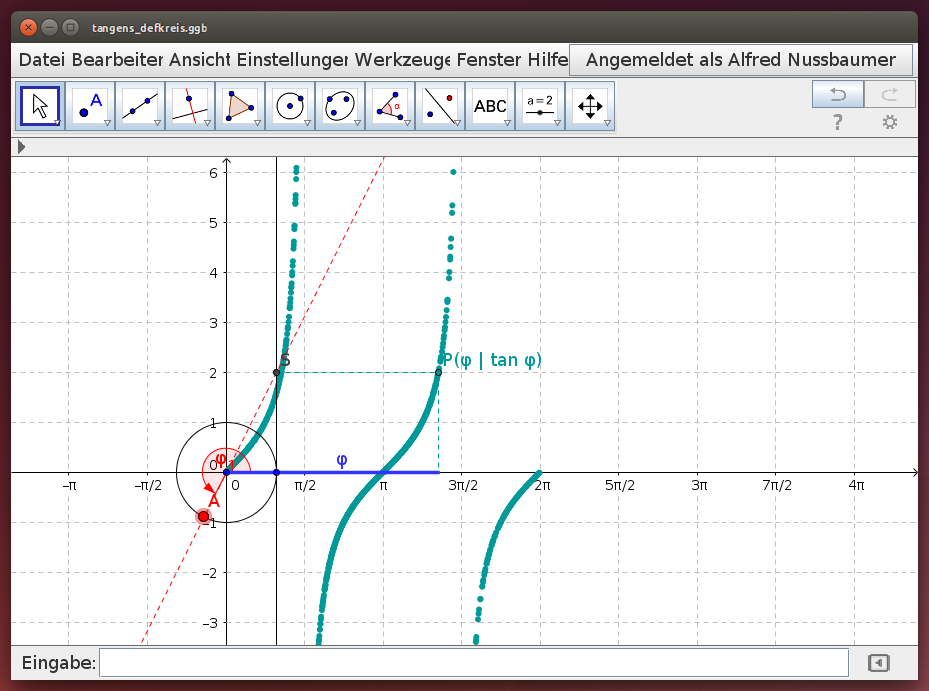
Tangensfunktion - Definition am Einheitskreis
Während du den roten Punkt A am Einheitskreis bewegst, ändern sich der Winkel φ und die y-Koordinate des Punktes S. Dieser Punkt S ist der Schnittpunkt der Geraden durch den Ursprung und den Punkt A mit der Tangente an den Einheitskreis. Der Winkel φ wird auf der x-Achse abgetragen: Die y-Koordinate des zugehörigen Punktes P entspricht der y-Koordinate von S.
Verschiebe im folgenden GeoGebra-Applet den roten Punkt S am Einheitskreis und beobachte die Spur von P:
Aufgaben:
- Lies die Tangenswerte für die Winkel φ = 90°, 180°, 270°, 360° ab und begründe ihre Werte!
- Begründe, warum die Tangensfunktion eine periodische Funktion ist! Gib die Periodenlänge an und vergleiche mit der Sinusfunktion