Rekursive Darstellung einer Folge

tm.jpg 6, S. 56 - 57

Bei der rekursiven Darstellung einer reellen Zahlenfolge ist der Anfangswert der Folge gegen. Das n-te Glied der Folge wird aus dem vorangegangenem Folgenglied berechnet:

tex:a_1, tex:a_n = T(a_{n-1})

Beispiel

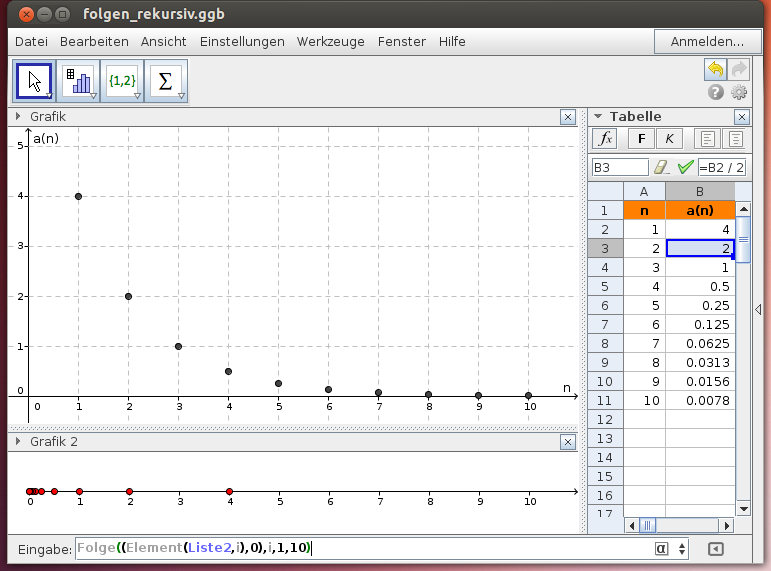
Wir berechnen die ersten 10 Folgenglieder der rekursiv definierten Folge: tex:a_1 = 4, tex:a_n = \frac {a_{n-1}} 2 und stellen die Folgenglieder in einem Koordinatensystem (n | a(n)) oder auf der Zahlengerade dar:

Screenshot: Alfred Nussbaumer

Download der GeoGebra-Datei

Hinweis: Rekursiv definierte Folgen werden vorteilhaft in der Tabellenansicht berechnet. Aus den beiden Tabellenspalten kann die Liste der Punkte für die Darstellung der Folge im (n|a(n)) - Koordinatensystem direkt erzeugt werden.

Für die Darstellung auf der Zahlengerade erzeugen wir aus der Spalte B eine Liste der Folgenwerte. Anschließend legen wir eine Liste von Punkten auf der Zahlengerade durch den Befehl

Folge((Element(Liste2,i),0),i,1,10)

fest und stellen die damit erzeugten Punkte im Grafik2-Fenster dar.

Anmerkung: Rekursiv definierte Folgen können auch mit dem GeoGebra-Befehl Iterationsliste(<Funktion>,<Anfangswert>,<Anzahl der Iterationen>) berechnet werden.

Zurück zu Folgen und Reihen


Zuletzt angesehen: • rekursive_darstellung_einer_folge