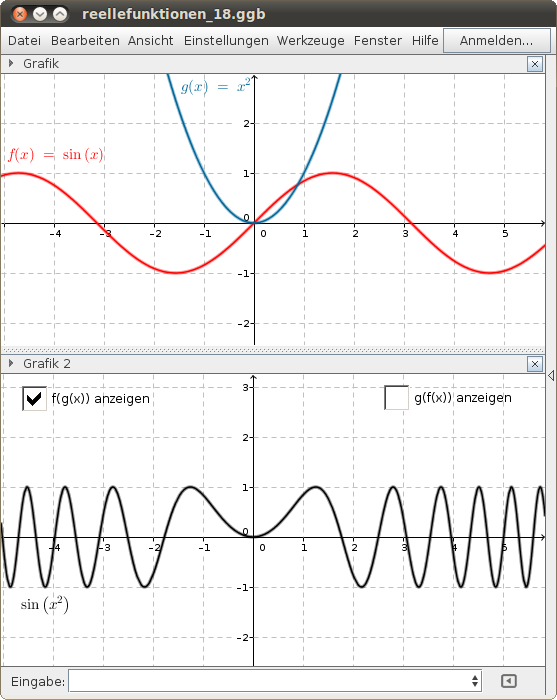
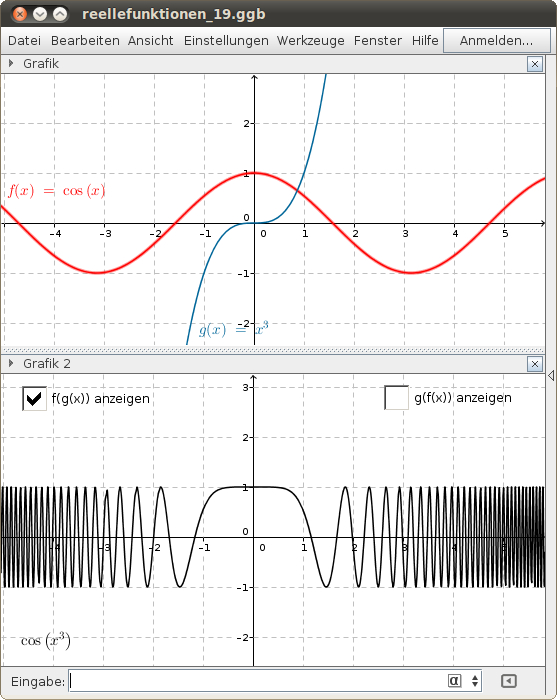
Zwei Funktionen verketten

tm.jpg 6, S. 156 - 157

Gegeben sind zwei Funktionen tex:f(x) = \sin (x) und tex:g(x) = x^2. Beschreibe die Funktionen f o g und g o f anhand des folgenden GeoGebra-Beispiels:

Screenshot: Alfred Nussbaumer

Download der GeoGebra-Datei

Aufgaben:

Hinweis: Gib die erforderlichen Definitionen der Funktionen f(x) und g(x) in der Eingabezeile ein.

  • Wähle die Funktionen tex:f(x) = x + 2 und tex:g(x) = 3 \cdot x und untersuche f o g und g o f anhand der Funktionsgraphen!
  • Wähle die Funktionen tex:f(x) = x - 1 und tex:g(x) = \cos (x) und untersuche f o g und g o f anhand der Funktionsgraphen!
  • Wähle die Funktionen tex:f(x) = \cos (x) und tex:g(x) = x^3 und untersuche f o g und g o f anhand der Funktionsgraphen!

Lösung:

Zurück zu Verketten von Funktionen | Reelle Funktionen


Zuletzt angesehen: • reellefunktionen_18