Parametergleichung
Du hast die Parameterform der Geradengleichung im Kapitel zur Analytischen Geometrie der Ebene kennen gelernt. Wir schreiben dazu die Koordinaten P(x|y) aller Punkte P, die auf der Geraden liegen, durch Parametergleichungen an, zB:
x(t) = 3 + 2 t y(t) = 5 + 3 t
GeoGebra stellt Geraden in Parameterdarstellung mit dem Befehl Kurve[x(t),y(t),t,a,b] dar - für den Parameter t werden Werte aus dem Intervall [a;b] eingesetzt.
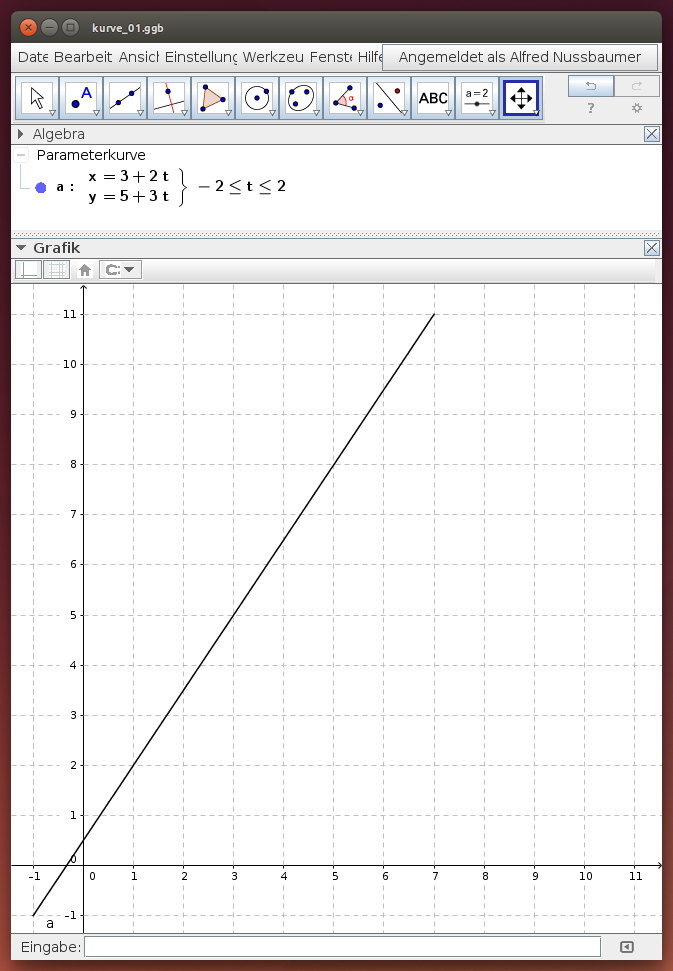
Im folgenden GeoGebra-Beispiel erhält der Parameter t die Werte aus dem Intervall [-2;2]. Für die oben angegebene Gerade ergibt sich somit der Befehl Kurve[3 + 2t, 5 + 3t, t, -2,2]:
Aufgaben:
- Gib weitere Geradengleichungen in Parameterform, auch zu verschiedenen Intervallen für den Parameter t, ein!
Du kannst alle Funktionen mit Hilfe von Parametergleichungen festlegen, beispielsweise für die Funktion f(x) = x²:
x(t) = t y(t) = t²
- Überprüfe dies im obigen GeoGebra-Beispiel, indem du einerseits die Funktionsgleichung
f(x) = x^2und andererseits die KurvendarstellungKurve[t,t^2,t,-2,2]]wählst und beide Graphen miteinander vergleichst!
Besonders interessant ist diese Darstellung bei parametrisierten Kurven.
Zurück zu Analytische Geometrie der Ebene