Lineare Gleichungssysteme mit Matrizen lösen

(zu tm.jpg Themenheft Angwandte Mathematik)

Bilden die Koeffizienten der Unbekannten eines (normierten) linearen Gleichungssystem eine reguläre Matrix M (d.h.: ist diese Matrix invertierbar), so hat das Gleichungssystem tex:M \cdot \vec X = \vec K die Lösung tex:\vec X = M^{-1} \cdot \vec K.

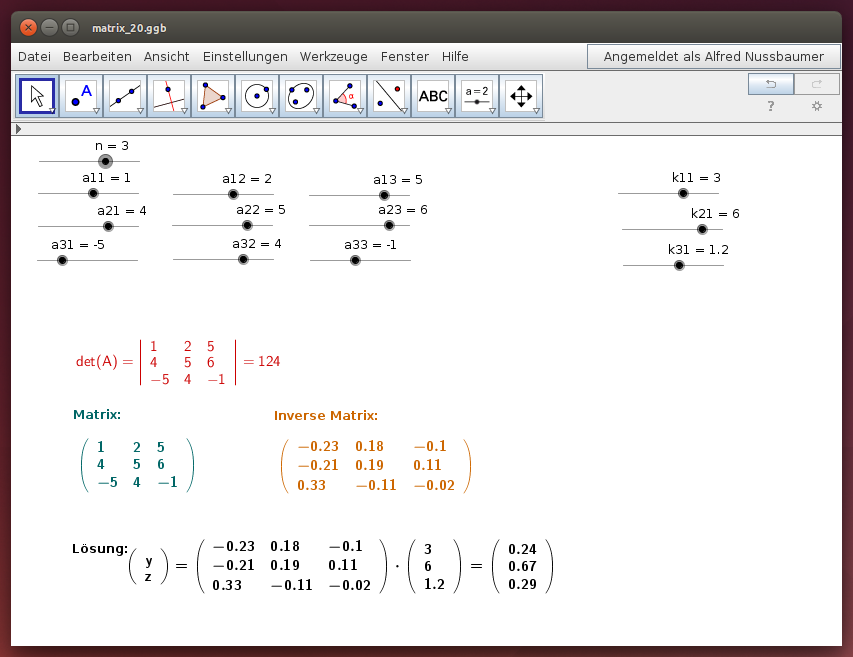
Lege im folgenden GeoGebra-Beispiel die Anzahl n der Unbekannten (n = 1, 2, 3, 4), die Koeffizienten und die Konstanten mit Hilfe der Schieberegler fest oder gib ihre Werte in der Eingabezeile ein. Lies die Lösungen der Gleichung aus dem Lösungsvektor tex:\vec X ab und kontrolliere durch Einsetzen:

Screenshot: Alfred Nussbaumer

Download der GeoGebra-Datei

Aufgaben:

  • Formuliere die Voraussetzungen dafür, dass das lineare Gleichungssystem lösbar ist (Hinweis: Anzahl der Unbekannten, Anzahl der Gleichungen, Determinante det(M) der Koeffizientenmatrix M)!

Zurück zu Matrizen


Zuletzt angesehen: • matrix_20