(zu )

Beim Hill-Verfahren werden Textblöcke mit Hilfe Matrizenoperationen verschlüsselt:

mod k, Der Schlüssel s besteht aus der Matrix A und dem Vektor B. Soll ein Text P mit der Blocklänge verschlüsselt werden, muss der Vektor B 5 Komponenten aufweisen, und die Matrix A muss eine 5 x 5 - Matrix sein.

Download der GeoGebra-Datei

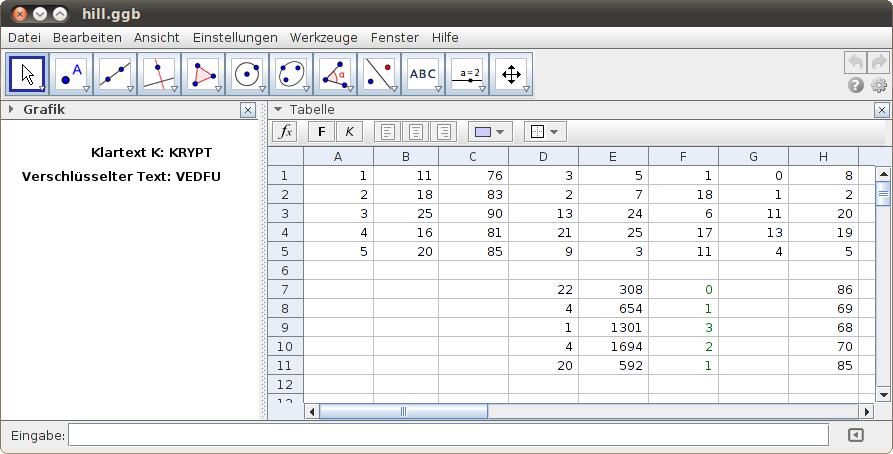
• Die Matrizenrechnungen wurden hier in der Tabellenkalkulation von GeoGebra umgesetzt, um die Restklassenarithmetik für alle Elemente der Matrizen anwenden zu können. Überprüfe die Formeln zur Multiplikation und Addition der Matrizen!
• Technologie: Das Hill-Verfahren kann mit Hilfe von Iteration auf beliebig lange Texte angewendet werden. Wie kann dies mit der GeoGebra-Funktion „Folge“ und der Tabellenkalkulation realisiert werden?
• Erstelle ein Modell, mit dem die verschlüsselten Texte nach dem Hill-Verfahren wieder entschlüsselt werden können!
• Recherchiere, ob das Hill-Verfahren auch mit Matrizen mit mehr als 5 Zeilen und Spalten realisiert werden kann …

Zurück zu Lernpfad Kryptographie | GeoGebra 3.2: Texte codieren, Listen bearbeiten, Restklassenarithmetik ... | Matrizen