a sin x + b cos x

(zu tm.jpg 6, S. 155)

Untersuche die Beziehung tex:a \cdot \sin (x) + b \cdot \cos (x) = A \cdot \sin (x + p) mit Hilfe der Parameter a, b, A und p!

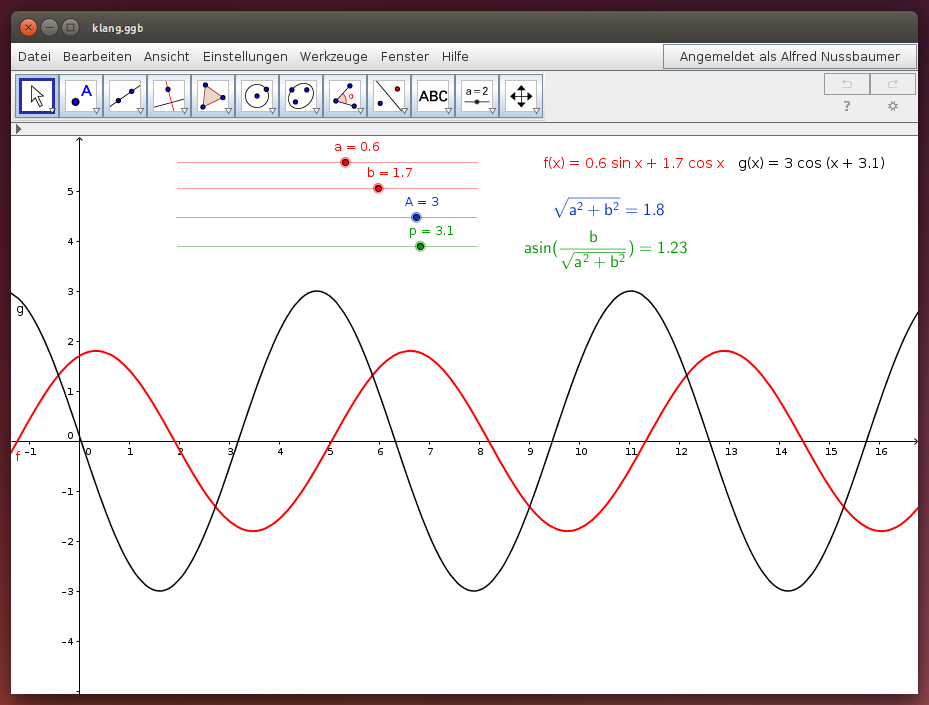
Wähle im folgenden GeoGebra-Applet die Funktion f(x) mit HIlfe der Schieberegler für a und b. Wähle anschließend passende Werte für die Parameter A und p so, dass die Kurve g(x) f(x) genau deckt!

Screenshot: Alfred Nussbaumer

Download der GeoGebra-Datei

Aufgaben:

  • Vergleiche die Werte der Parameter A und p mit den berechneten Werten!
  • Vergleiche die Frequenzen der Summanden mit der Frequenz des Ergebnisses!
  • Untersuche die trigonometrische Herleitung mit Hilfe von Zeigerdiagrammen!
  • Ausblick: Was hat das mit Schwingungen in der Musik zu tun?

Algebraische Herleitung:


Zuletzt angesehen: • klang