Inhaltsverzeichnis
Der Grenzwert einer Folge
Wenn für jeden (noch so kleinen) Abstand ε ab einem (großen) n der Betrag |an - a| < ε bleibt, so heißt a der Grenzwert der Folge <an>.
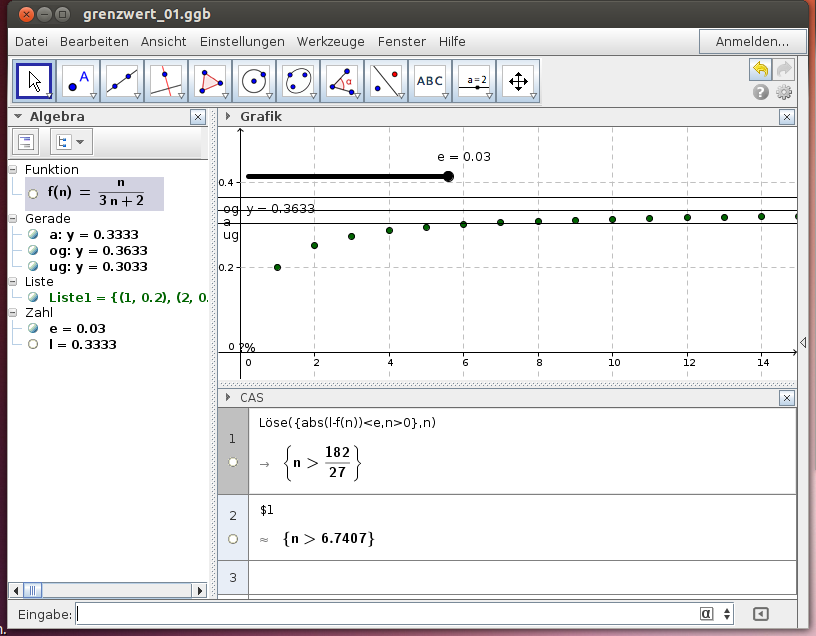
Hinweis: Im folgenden GeoGebra-Beispiel werden die Folgenglieder <an> mit der Funktion f(n) berechnet. Der Grenzwert l wird mit dem GeoGebra-Befehl Grenzwert(<Funktion>,∞) bestimmt.
Beispiel 1:
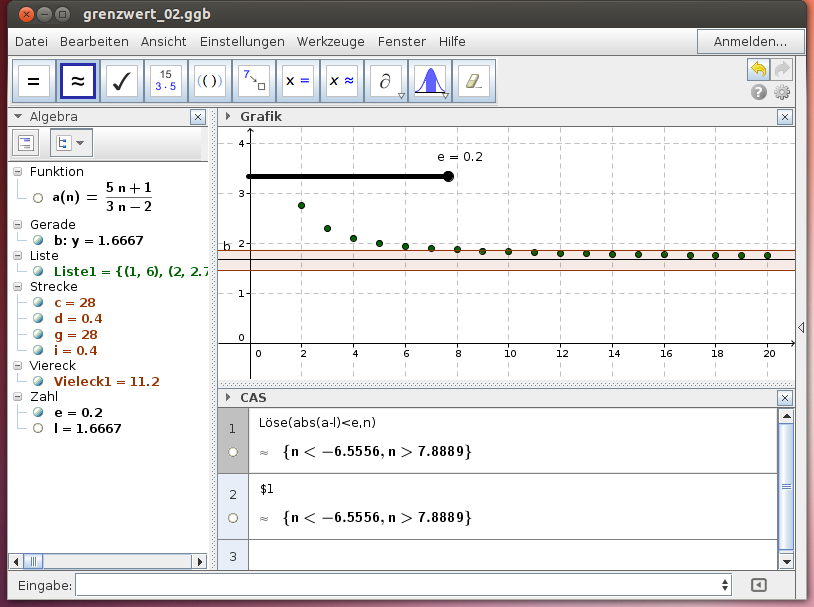
Beispiel 2:
Aufgaben:
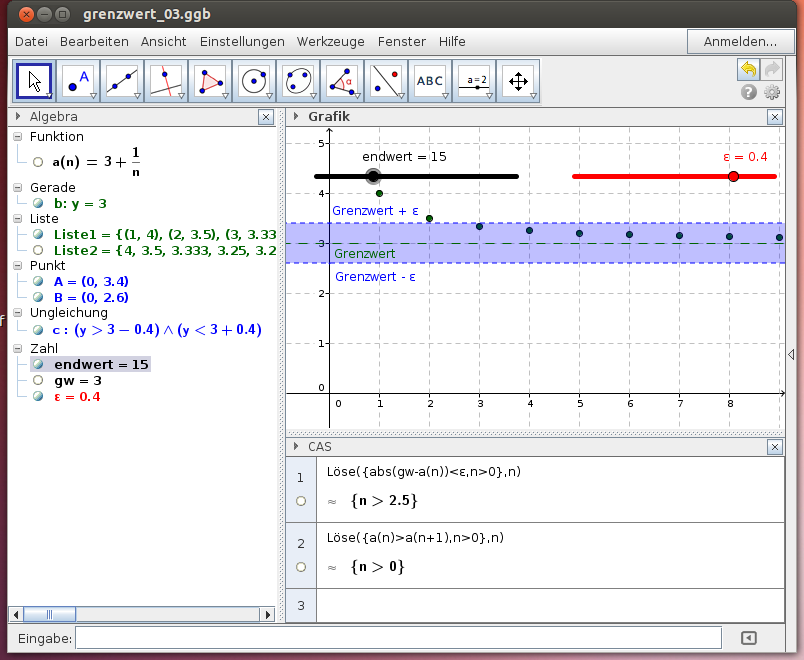
- Untersuche die Folge an = 3 + 1/n: Bestimme den Grenzwert und ermittle den Index n, ab dem alle weiteren Folgenglieder näher zum Grenzwert liegen als 0,4! Überprüfe das Monotonieverhalten der Folge!
- Wähle weitere Folgenglieder durch Eingabe eines Ausdrucks für a(n) in die Eingabezeile, berechne den Grenzwert und bestimme für verschiedene (kleine) Abstände e vom Grenzwert den Folgenindex, ab dem alle weiteren Folgenglieder in der Nähe des Grenzwertes liegen!
- Löse die entsprechenden Ungleichungen in der CAS-Ansicht und interpretiere die Ergebnisse!
- Technologie: Untersuche den GeoGebra-Befehl
Grenzwert()!
Zurück zu Folgen und Reihen