Glücksspiele
(zu 
7, S. 30 - 31)
Es gilt zahlreiche Arten von Glücksspielen, die sich unter Anderem dadurch unterscheiden, ob der Spieler / die Spielerin der Verlauf eines Glücksspiels auch durch eigenes Geschick variieren kann, etwa durch geschicktes bzw. ungeschicktes Setzen der Spielkegel beim Würfelspiel „Mensch ärgere dich (nicht)“ …
- Vergleiche die Glücksspiele mit kombinatorischen Spielen (z.B. Nim, Schach) und mit strategischen Spielen (Dame, Go)!
Eine besondere Bedeutung erhalten Glücksspiele, wenn Geldbeträge eingesetzt und - bei Gewinn - ausbezahlt werden (vgl. 7 S. 30,31).
Zahlreiche Varianten lassen Kartenspiele zu, sie werden beispielsweise nach dem Spielziel in Ablegespiele, Stichspiele, Augenspiele oder Anlegespiele eingeteilt.
Überlegungen zum Würfeln
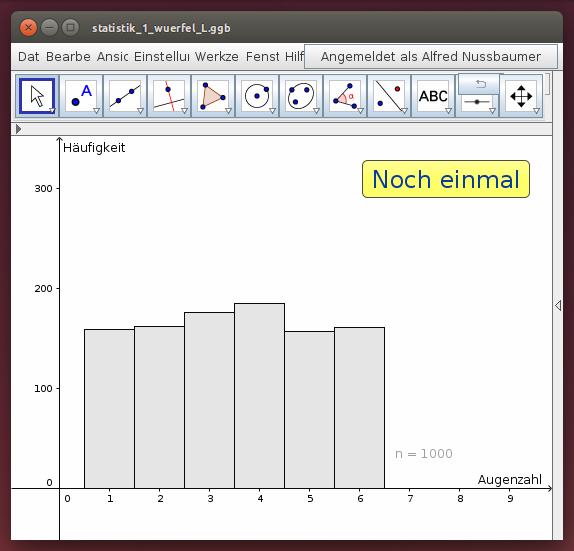
- Gib an, wie oft bei 1000 Würfen die Augenzahl 1, 2, 3, 4, 5 oder 6 fallen wird!
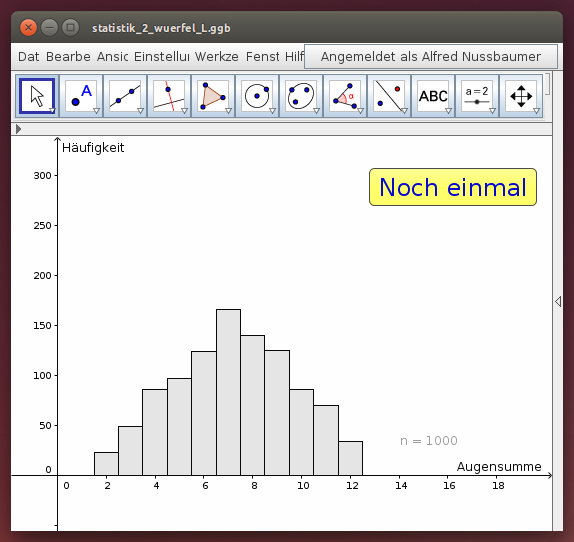
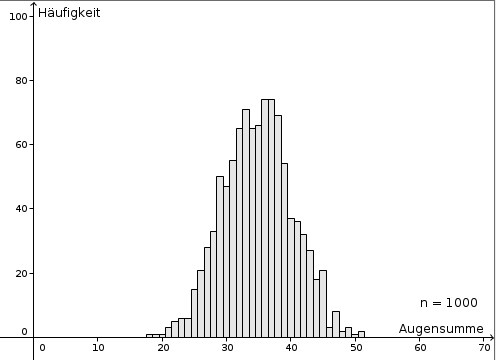
- Würfelt man (gleichzeitig) mit 2 Würfeln, so ist die Augensumme für den Spielverlauf ausschlaggebend. Untersuche, wie häufig bei 1000 Würfen die Augensumme 2, 3, 4, … 12 auftritt!
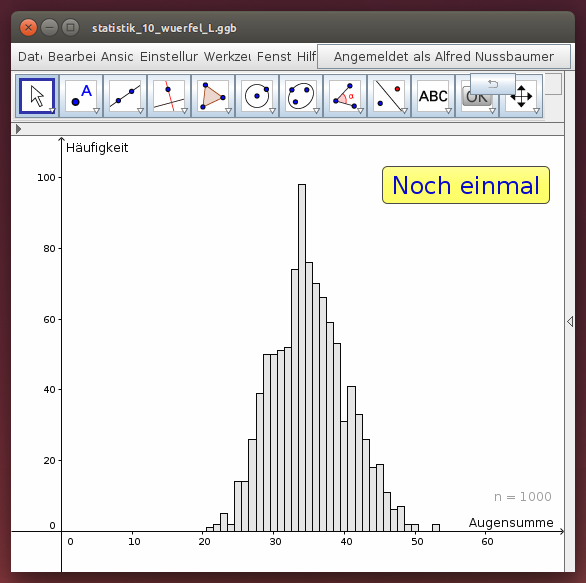
- Vergleiche das Ereignis der Augensumme von 2 Würfeln mit der Augensumme von 10 Würfeln. Ändert sich die Form des Häufigkeitsdiagramms?
Anmerkung: Die obigen GeoGebra-Beispiele verwenden für die Zwischenergebnisse der Würfe Listen. Du kannst die Aufgaben auch mit der Tabellenansicht lösen.
Weitere Aufgaben
- Erstelle Häufigkeitsdiagramme für das Würfeln mit 4, 5, … Würfeln!
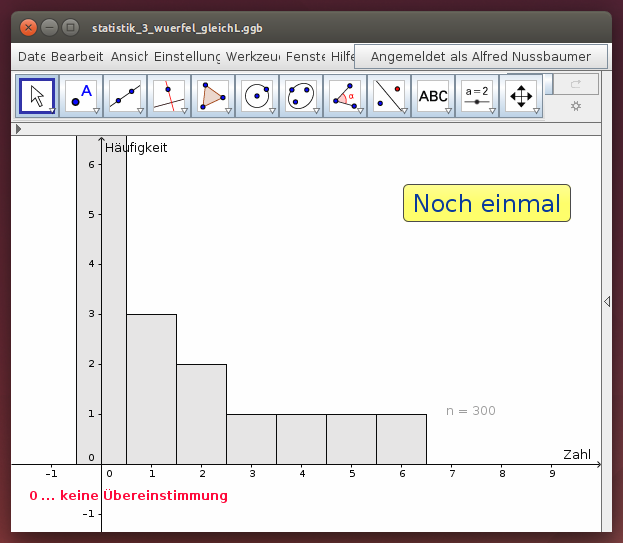
- Erstelle Häufigkeitsdiagramme für das Ereignis, dass beim Würfeln mit 3 Würfeln alle 3 Würfel die gleiche Augenzahl 1, 2, 3, 4, 5, oder 6 haben und vergleiche mit dem Würfeln mit einem einzigen Würfel!
- Berechne die Wahrscheinlichkeiten für alle Würfelereignisse dieser Seite und vergleiche mit den Häufigkeitsdiagrammen!
Rechtliches
- Informiere dich über rechtliche Grundlagen zu Glücksspielen!
- Beschreibe, was ein Gewinnspiel gegenüber einem Glücksspiel abgrenzt!
Historisches
- Recherchiere zu den Würfelspielen der Antike!
- Untersuche die geschichtliche Entwicklung von Kartenspielen!
- Recherchiere zur Geschichte des Glücksspiels Roulette!
Ausblick
- Informiere dich über das Problem des Chevaliers de Méré!
