Gleichungssysteme mit unendlich vielen Lösungen

6, S. 30 - 31

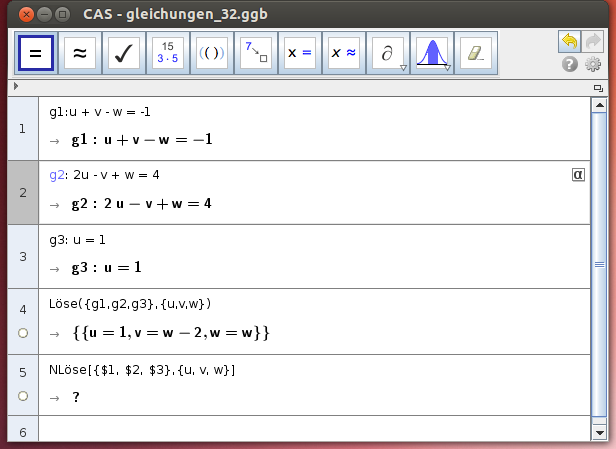
• Löse das lineare Gleichungssystem:

 u + v - w = -1
2u - v + w = 4
 u         = 1
 

(Anmerkung: Der Befehl NLöse() liefert kein Ergebnis für das Gleichungssystem)

• Interpretiere das obige Ergebnis!

Lösung:

• Die Gleichungen des obigen Systems sind nicht voneinander unabhängig. Suche nach Abhängigkeiten!

Lösung:

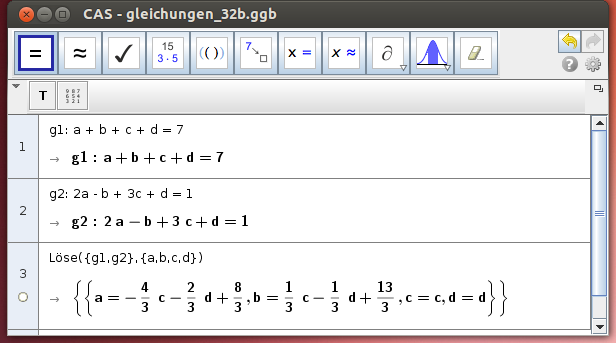
• Löse das Gleichungssystem:

 a + b +  c + d = 7
2a - b + 3c + d = 1

Beachte: Da das Gleichungssystem 4 Unbekannte, aber nur 2 Gleichungen aufweist, können zwei Unbekannte, z.B. c und d, frei gewählt werden. Es liegt eine 2-parametrige Lösung vor.

Zurück zu Gleichungen und Ungleichungen