Das Geburtstagsproblem

tm.jpg, Angewandte Mathematik, Kryptographie

Aufgabe:

  • Wie groß ist die Wahrscheinlichkeit, dass von n zufällig anwesenden Personen mindestens zwei am selben Tag Geburtstag haben?

Insgesamt gibt es 365n Möglichkeiten, an einem Tag im Jahr Geburstag zu haben.

Wir rechnen mit der Gegenwahrscheinlichkeit: Kennen wir den Geburtstag für eine Person, also einen bestimmten Tag im Jahr, so bleiben für alle anderen Personen nur 364 Tage zur Auswahl - so dass, keine zweite Person an diesem Tag Geburtstag hat. Für n Personen somit tex:\frac {364^n}{365^n} Möglichkeiten.

Für die gesuchte Wahrscheinlichkeit erhalten wir somit: tex:p = 1 - \frac {364^n}{365^n}

Aufgabe:

  • Wie groß ist die Wahrscheinlichkeit, dass von n zufällig anwesenden Personen zwei Personen an irgendeinem Tag (im Jahr) gemeinsam Geburtstag haben?

Richtig: Wir bilden das Gegenereignis „alle Geburtstage für n Personen sind verschieden“:

tex:365 \cdot 364 \cdot \dots \cdot (365 - n + 1) = \frac {365!} {(365-n)!}

Für die gesuchte Wahrscheinlichkeit erhalten wir somit: tex:p = 1 - \frac{\frac {365!} {(365-n)!}}{365^n}

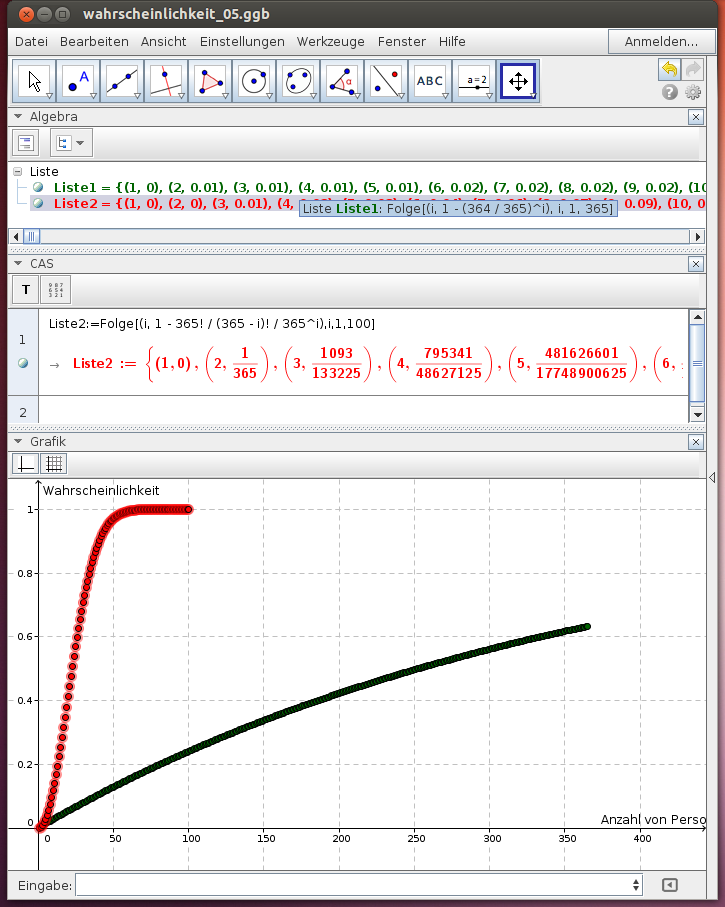
Wir stellen die berechneten Wahrscheinlichkeiten für 1, 2, 3, … n Personen dar:

Screenshot: Alfred Nussbaumer

Download der GeoGebra-Datei

Zurück zu Lernpfad Kryptographie | GeoGebra 3.2: Texte codieren, Listen bearbeiten, Restklassenarithmetik ... | WS2.3


Zuletzt angesehen: • geburtstagsproblem