Tangente und Normale an die Exponentialfunktion
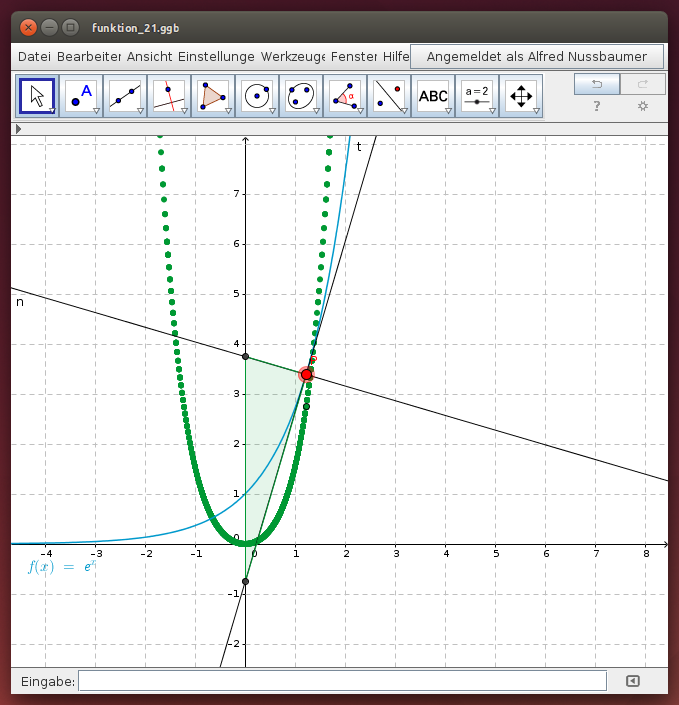
Lege in einem Punkt P der Exponentialfunktion f(x) = ex die Tangente und die Normale. Diese beiden Geraden bilden gemeinsam mit der y-Achse ein (rechtwinkliges) Dreieck. Untersuche den Flächeninhalt dieses Dreiecks in Abhängigkeit von der x-Koordinate des Punktes P!
Verschiebe im folgenden GeoGebra-Applet den roten Punkt P entlang der Exponentialfunktion. Der Flächeninhalt des zugehörigen rechtwinkligen Dreiecks wird als Punktespur dargestellt. Beschreibe die Eigenschaften der dadurch entstehenden Funktion!
Aufgaben:
- Untersuche ob die Funktion des Flächeninhalts symmetrisch zur y-Achse ist. Begründe dies rechnerisch!
- Formuliere eine analoge Aufgabe für die Logarithmusfunktion f(x) = ln x!
Zurück zu Eigenschaften von Funktionen