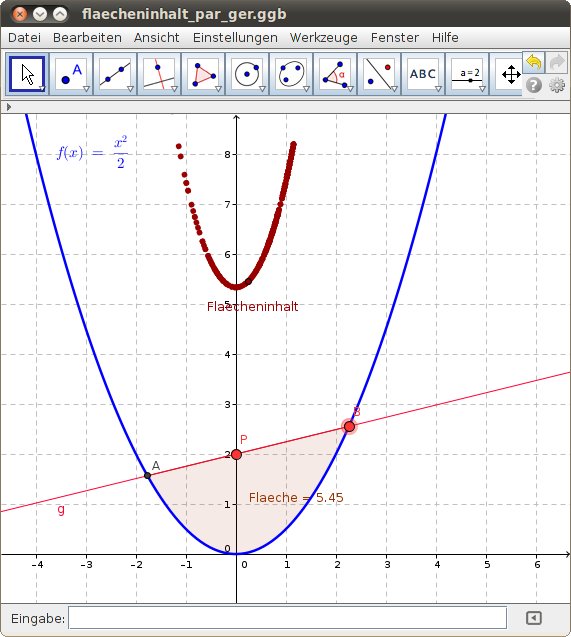
Zum Inhalt einer Fläche zwischen Parabel und Gerade
Wir untersuchen den Inhalt der Fläche, die zwischen der Parabel und der linearen Funktion
liegt. Bei welcher Lage der Geraden ist der Flächeninhalt am kleinsten?
Verschiebe im folgenden GeoGebra-Applet den Punkt B auf der Parabel (dabei ändert sich die Steigung k der Geraden) und beoachte den Flächeninhalt:
Aufgaben:
- Formuliere eine analoge Aufgabenstellung für einen Rechteckstreifen und beschreibe das Ergebnis (Lösungsvorschlag)!
- Verschiebe den Punkt P auf der senkrechten Achse (dabei ändert sich das d der Geraden): Was ändert sich dabei für die obigen Aufgabenstellung?
- Übertrage die Situation auf den Raum: Statt der Parabel liegt dann ein Paraboloid, statt der Geraden eine Ebene vor. Formuliere eine Aufgabenstellung f\“ur den Rauminhalt des Schnittkörpers!
- Die analoge Aufgabenstellung im Raum: Ein Drehzylinder / ein elliptischer Zylinder / ein Quader / … wird von einer Ebene geschnitten. Was lässt sich für das Volumen des Schnittkörpers aussagen, wenn die Ebene um einen Punkt der Zylinderachse / der Symmetrieachse des Quaders gedreht wird?
Zurück zu Flächeninhalt unter einer Kurve | Anwendungen der Integralrechnung