Flächenberechnungen
Wir berechnen Flächeninhalte von Dreiecken, Vierecken, … Vielecken mit Hilfe von Dreiecksflächen.
Für den Inhalt einer Dreiecksfläche verwenden wir beispielsweise
- die trigonometrische Flächenformel (
)
- die vektorielle Flächenformel (
).
Hinweis: Rechne die Kontrolle mit Hilfe des Flächeninhalts-Werkzeuges!
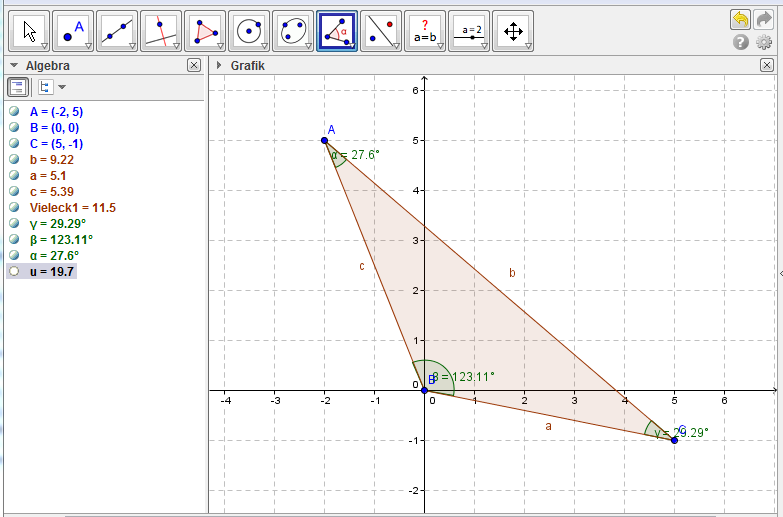
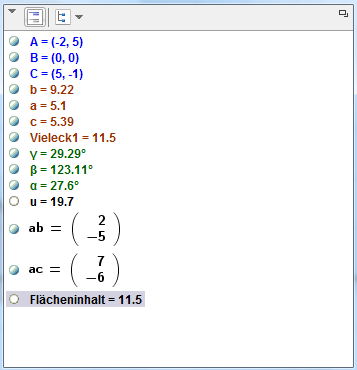
Beispiel:
Berechne den Umfang, den Flächeninhalt und alle Winkel des Dreiecks A(-2|5), B(0|0), C(5|-1)!
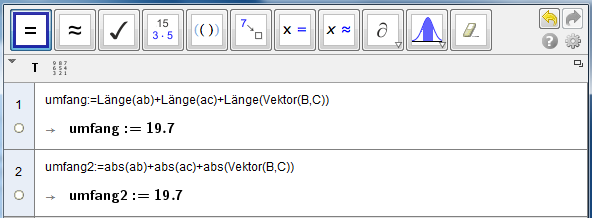
Im CAS-Fenster kann für die Länge von Vektoren entweder der Befehl Länge() oder die Betragsfunktion abs() verwendet werden:
Länge eines Vektors im CAS-Fenster:
Zurück zu Vektorrechnung