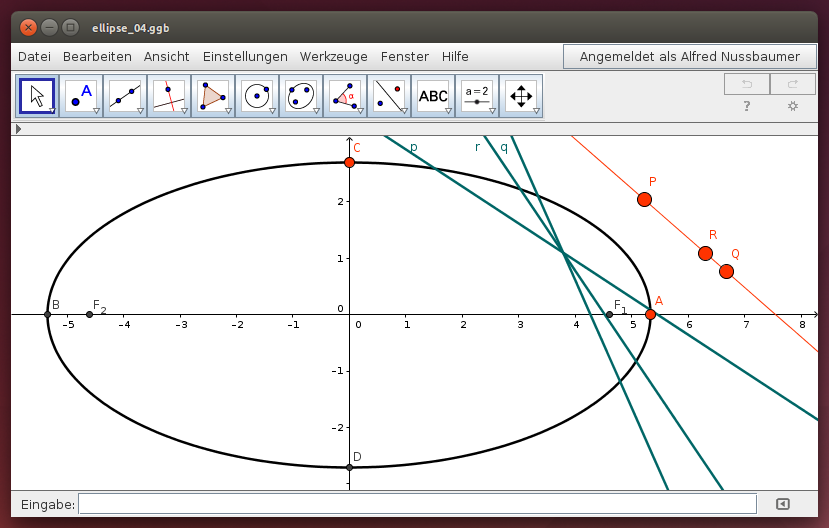
Ellipse: Pol und Polare
Zu drei roten Punkten P, Q und R wurden die zugehörigen Polaren p, q und r konstruiert. Verschiebe einen der drei Pole und beobachte, wie sich die zugehörige Polare verändert!
Aufgaben:
- Überprüfe: Die Polaren zu drei Punkten, die auf einer Geraden liegen, schneiden einander in einem Punkt!
- Überprüfe: Die Polare eines gemeinsamen Punktes mehrerer Polaren ist eine Gerade, die alle Pole der betrachteten Polaren enthält!
- Verschiebe die Pole so, dass sie innerhalb der Ellipse liegen und überprüfe die obigen Sätze zu Pol und Polare!
zurück zu Kegelschnittslinien | Nichtlineare analytische Geometrie (R2)