Der Differenzenquotient

tm.jpg 7, S. 38-39

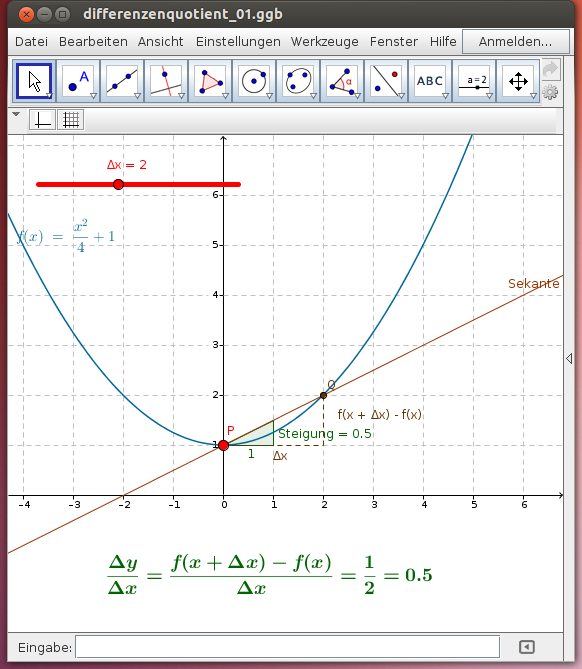
Der Differenzenquotient bedeutet geometrisch das Seitenverhältnis tex:\frac {\Delta y} {\Delta x} im Steigungsdreieck; die mittlere Änderungsrate der Funktionswerte.

Im folgenden GeoGebra-Beispiel ist das Steigungsdreieck der Sekante an die Kurve tex:y = \frac {x^2} 4 + 1 durch die Punkte P und Q eingezeichnet. Die x-Koordinate des Punktes Q unterscheidet sich von der x-Koordinate des Punktes P um die Differenz tex:\Delta x …

Screenshot: Alfred Nussbaumer

Download der GeoGebra-Datei

Aufgaben:

  • Wähle verschiedene Positionen des Punktes P und interpretiere den Wert des Differenzenquotienten!
  • Wähle verschiedene Werte für tex:\Delta x und interpretiere den Wert des Differenzenquotienten!
  • Untersuche und beurteile: Kann der Differenzenquotient auch negativ sein? Begründe deine Antwort!

Zurück zu Grundlagen der Differentialrechnung | AN1.3


Zuletzt angesehen: • differenzenquotient_01