Ableitungsfunktion
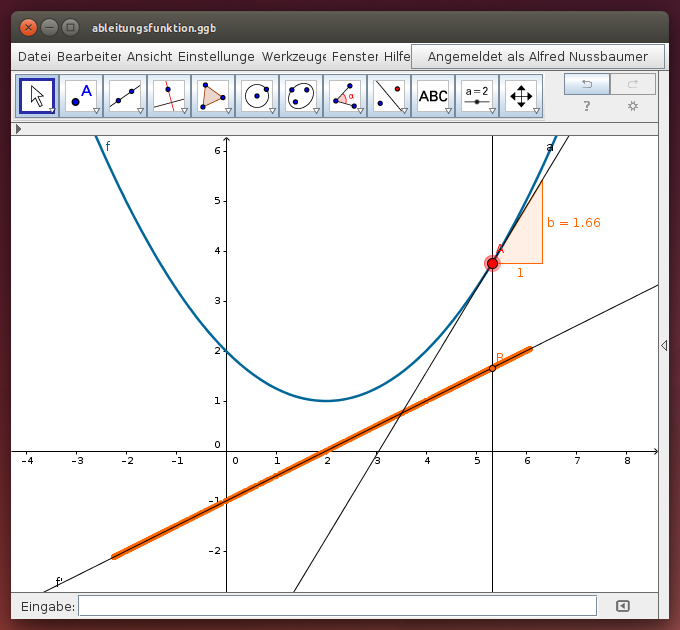
Gegeben ist die (quadratische) Funktion f(x). Verschiebe den roten Punkt A auf dem Funktionsgraphen von f und beobachte die Steigung der Tangente im Punkt A! Wir stellen zu jeder Position des Punktes A die zugehörige Steigung als Punktespur dar …
Die Punktespur ist die Ableitungsfunktion f'(x) der Funktion f(x).
Aufgaben:
- Gib (in der Eingabezeile) andere Funktionsterme für f(x) ein, z.B.
,
und interpretiere die Ableitungsfunktion!
Zurück zu Grundlagen der Differentialrechnung | AN3.1 | AN3.2