Inhaltsverzeichnis
Der Schrägriss
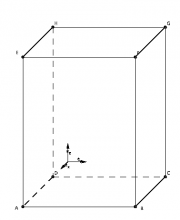 Mit dem Schrägriss stellst du Körper auf einem (ebenen) Zeichenblatt dar.
Mit dem Schrägriss stellst du Körper auf einem (ebenen) Zeichenblatt dar.
Eine einfache Methode besteht darin, dass die y-z-Ebene in wahrer Größe dargestellt wird. Dies gelingt, wenn die y-Achse und die z-Achse parallel zum Zeichenblatt liegen. Die x-Achse wird nun (beispielsweise) um 45° gegen die horizontale y-Achse geneigt und verkürzt gezeichnet.
Beispiel: GeoGebra
Mit GeoGebra lassen sich Prismen und Pyramiden mit Hilfe geeignet gewählter Achsenvektoren des räumlichen Koordinatensystems leicht zeichnen. Wir verwenden dazu die x-Achse von GeoGebra als y-Achse, die y-Achse von GeoGebra ist die z-Achse. Blickst du „schräg“ auf das räumliche Koordinatensystem, so erscheint die x-Achse schräg und verkürzt.
Deklariere die Achsenvektoren in der GeoGebra-Eingabezeile:
e_x = (-0.4,-0.4) e_y = (1,0) e_z = (0,1)
Möchtest du den Punkt P(2|-3|5) mit diesen Achsenvektoren darstellen, so addierst du ihre entsprechenden Vielfachen:
P = 2 e_x - 3 e_y + 5 e_z
GeoGebra 3D
GeoGebra 3D bietet die Darstellung räumlicher Objekte im Schrägriss in der Ansicht Grafik 3D. Lies Grundlagen dazu im Abschnitt Analytische Geometrie des Raumes nach!
