Inhaltsverzeichnis
Wie berechenbar sind deine Konstruktionen?
 Mit Zirkel und Linear hast du in den letzten Jahren zu konstruieren gelernt. Viele Zeichnungen hast du dabei wahrscheinlich auch mit einem Geometrieprogramm (zB GeoGebra) bewältigt. Hast du dir schon einmal überlegt, dass jede Konstruktion, die mit dem Computer ausgeführt und dargestellt wird, bis ins letzte Detail berechnet werden muss?
Mit Zirkel und Linear hast du in den letzten Jahren zu konstruieren gelernt. Viele Zeichnungen hast du dabei wahrscheinlich auch mit einem Geometrieprogramm (zB GeoGebra) bewältigt. Hast du dir schon einmal überlegt, dass jede Konstruktion, die mit dem Computer ausgeführt und dargestellt wird, bis ins letzte Detail berechnet werden muss?
In der 5. Klasse und in der 6. Klasse behandelst du Punkte, Geraden und ebene Flächen. Die Berechnung von Kreisen, Ellipsen, Hyperbeln, Parabeln oder Kugeln ist erst Thema der 7. Klasse. Hier behandeln wir deshalb ausschließlich Konstruktionen für Polygone: Von einem Dreieck beispielsweise können wir in der 5. Klasse die Seitenlängen, Winkel, Flächeninhalt, den Schwerpunkt, später auch die Streckensymmetralen, den Umkreismittelpunkt und den Umkreisradius bestimmen, nicht aber eine Gleichung für die Kreislinie selbst angeben.
Aufgaben
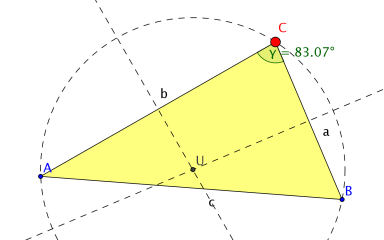
- Ergänze Berechnungen am Dreieck, die du mit dem Wissen der 5. Klasse noch ausführen kannst!
- Zeichne ein Rechteck mit den Seitenlängen a = 8 cm und b = 6 cm und untersuche Eigenschaften und Gesetzmäßigkeiten, die du mit Zirkel und Lineal konstruieren kannst! Welche von diesen kannst du jetzt schon berechnen?
- Skizziere ein Parallelogramm und stelle alle möglichen Berechnungen (beispielsweise mit einer Mindmap) übersichtlich dar!
- Überlege Konstruktionen, die du in der Unterstufe am Kreis kennengelernt hast. Welche kannst du ohne das Wissen um die „Kreisgleichung“ schon jetzt, in der 5. Klasse, berechnen?
Bei den folgenden Aufgaben kannst du die Lösung mit Hilfe elementarer Konstruktionen finden. Im Vordergrund steht jedoch die rechnerische Lösung:
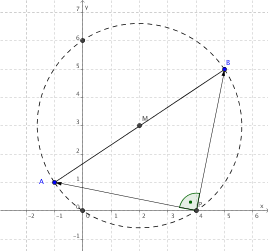
Sehwinkel
Von welchen Punkten der x-Achse aus erscheint die Strecke AB[A(-1/1), B(5/5)] unter einem rechten Winkel?
Sehwinkel
Von welchen Punkten der y-Achse aus erscheint die Strecke AB[A(-1/1), B(5/5)] unter einem rechten Winkel?
Ausblick
- Analytische Geometrie des Raumes (6. Klasse)
- Nichtlineare analytische Geometrie des Raumes (7. Klasse)
Studium
- Darstellende Geometrie
- Vermessungswesen
- Architektur
- Technische Zeichnerin / Technischer Zeichner
- Designer / Designerin
Zurück zu Analytische Geometrie der Ebene