Inhaltsverzeichnis
Biomathematik
Mathematische Modelle und Strukturen beschreiben die Dynamik lebender Systeme. Lies zu den Wachstumsmodellen nach, bevor du die Anwendungen auf dieser Seite bearbeitest!
Räuber-Beute-Modelle
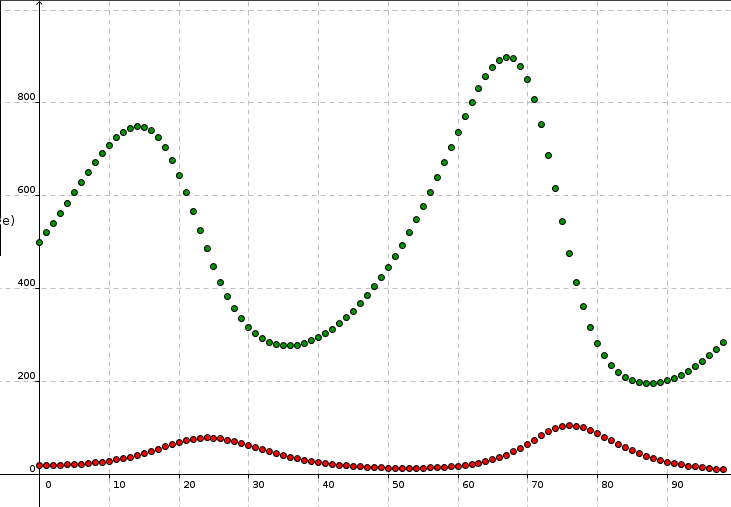
In Räuber-Beute-Modellen wird die Populationsdynamik von Beutetieren und Räubern mathematisch behandelt. Die Änderungsraten werden für die Anzahl der Beutetiere wie auch für die Räuber aus der aktuellen Anzahl von Beutetieren und Räubern sowie aus den entsprechenden Reproduktions- und Sterbefaktoren berechnet. Beispielsweise ergibt sich für ein Modell von Hasen und Füchsen pro Zeitschritt:
Hn+1 = Hn + e1 Hn - g1 Hn Fn
Fn+1 = Fn - e2 Fn + g2 Hn Fn
e1 … Reproduktionsrate der Hasen
e2 … Sterberate der Füchse
g1 … Sterberate der Hasen (pro jagenden Fuchs)
g2 … Reproduktionsrate der Füchse (pro gefressenen Hasen
Für e1 = 0.08, e2 = 0.2, g1 = 0.002, g2 = 0.0004 erhalten wir für anfänglich 500 Hasen und 20 Füchse die folgende Populationsdynamik.
Aufgabe
Untersuche die Dynamik eines Räuber-Beute-Systems anhand des GeoGebra-Modells Füchse und Hasen!
Epidemien
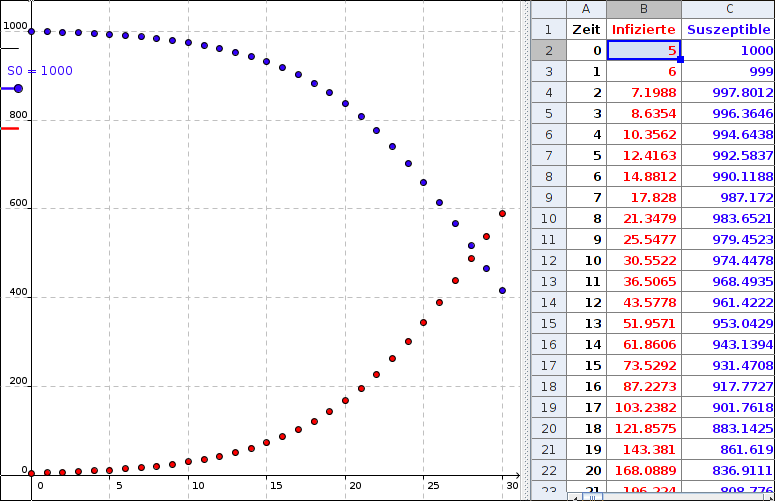
Ein wichtiges Teilgebiet der Biomathematik stellt die Epidmiologie dar. Dabei soll die Ausbreitung von Infektionskrankheiten in einer Population berechnet und bewertet werden.
Lies dazu in  6, Seite 188 und 189 nach!
6, Seite 188 und 189 nach!
Wir gehen von einer Anfangszahl I0 infizierter Personen und von einer Anfangszahl S0 suszeptibler Personen (gesunde Personen, die von der Krankheit befallen werden können) aus. Der Parameter p legt fest, wie viele suszeptible Personen von einer infizierten pro Zeiteinheit angesteckt werden:
Aufgabe
Untersuche die Dynamik der Ausbreitung der Infektionskrankheit mit dem GeoGebra-Modell Epidemie !
Künstliches Leben
Game of Life
Zelluläre Automaten
Zelluläre Automaten beschreiben dynamische Systeme, bei denen der Zustand einer Zelle von den Zuständen benachbarter Zellen im vorangegangenen Zeitschritt abhängen.
Untersuche den eindimensionalen zellulären Automaten nach Stephen Wolfram. Im folgenden Bild verläuft die Zeitachse von oben nach unten, die Zellen sind stets in einer horizontalen Geraden angeordnet:
Aufgabe:
- Untersuche eindimensionale zelluläre Automaten mit einem JAVA-Applet !
Ausblick
- Lotka-Volterra-Gleichungen