Füchse und Hasen (ein Räuber-Beute-Modell)
In Räuber-Beute-Modellen wird die Populationsdynamik von Beutetieren und Räubern mathematisch behandelt. Die Änderungsraten werden für die Anzahl der Beutetiere wie auch für die Räuber aus der aktuellen Anzahl von Beutetieren und Räubern sowie aus den entsprechenden Reproduktions- und Sterbefaktoren berechnet. Beispielsweise ergibt sich für ein Modell von Hasen und Füchsen pro Zeitschritt:
Hn+1 = Hn + e1 Hn - g1 Hn Fn
Fn+1 = Fn - e2 Fn + g2 Hn Fn
e1 … Reproduktionsrate der Hasen
e2 … Sterberate der Füchse
g1 … Sterberate der Hasen (pro jagenden Fuchs)
g2 … Reproduktionsrate der Füchse (pro gefressenen Hasen)
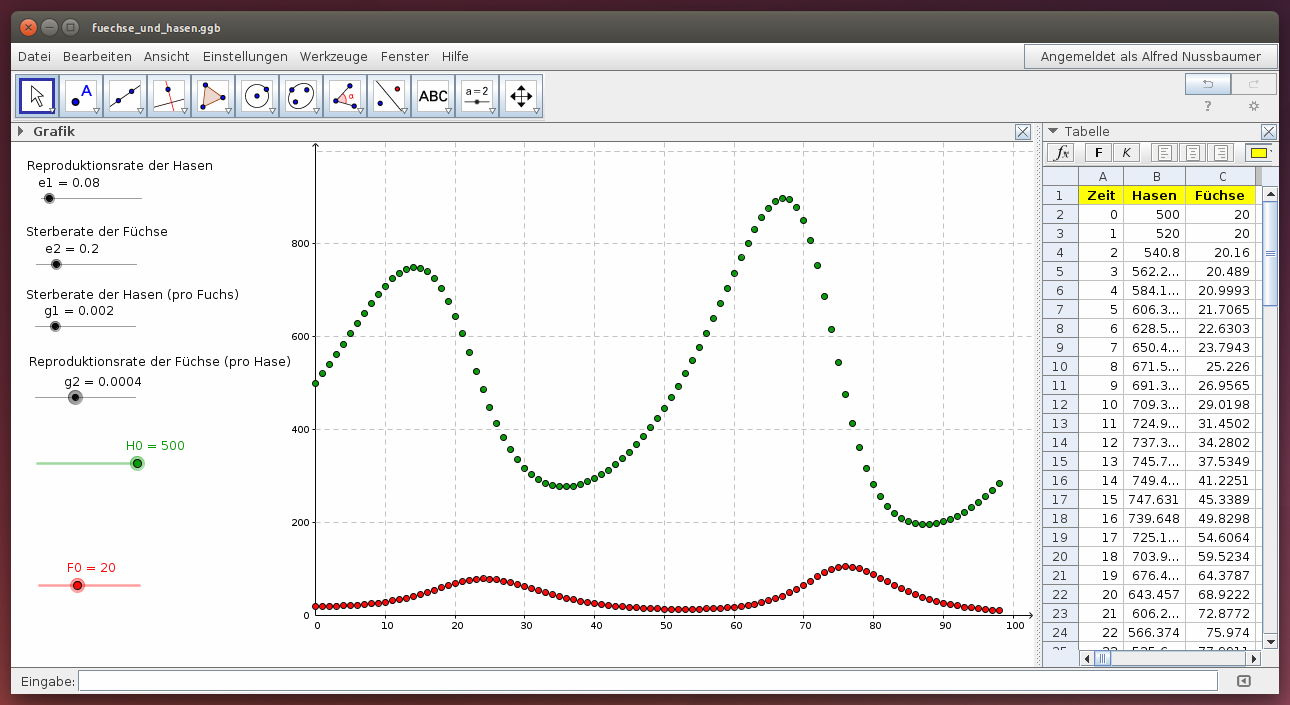
Im folgenden GeoGebra-Beispiel wird die Entwicklung für anfänglich 500 Hasen und 20 Füchse dargestellt. Variiere die Anfangszahlen mit den beiden Schiebereglern für H0 und F0 und interpretiere die sich daraus ergebenden Veränderungen:
Aufgaben
- Untersuche, welche Auswirkung eine (geringe) Änderung der Reproduktionsrate e1 der Hasen auf die Populationsdynamik hat!
- Untersuche, welche Auswirkung eine (geringe) Änderung der Sterberate e2 der Füchse auf die Populationsdynamik hat!
- Untersuche, welche Auswirkung eine (geringe) Änderung der Sterberate (pro Fuchs) g1 der Hasen auf die Populationsdynamik hat!
- Untersuche, welche Auswirkung eine (geringe) Änderung der Reproduktionsrate (pro gefressenen Hasen) g2 der Füchse auf die Populationsdynamik hat!
- Die obigen Differenzengleichungen leiten sich aus den Lotka-Volterra Gleichungen ab. Recherchiere dazu in der Schulbibliothek oder im Internet!
Zurück zur Themenseite Biomathematik