Inhaltsverzeichnis
Abstand eines Punktes von einer Geraden
Der Abstand eines Punktes P von einer Geraden g ist der Normalabstand des Punktes von der Geraden. Lege dazu eine Normalebene auf die Gerade g durch den Punkt und bestimmte den Abstand des Punktes vom Durchstoßpunkt der Geraden mit der Normalebene!
Beispiel: Bestimme den Abstand des Punktes P(0|5|4) von der Geraden g[A(2|1|9), B(4|0|11)]!
Lösung in der Grafikansicht Grafik 3D
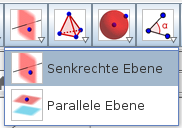
Gib die Punkte in der Eingabezeile ein, bestimme die Geraden mit dem Geraden-Werkzeug und die Normalebene mit dem Werkzeug „Senkrechte Ebene“:
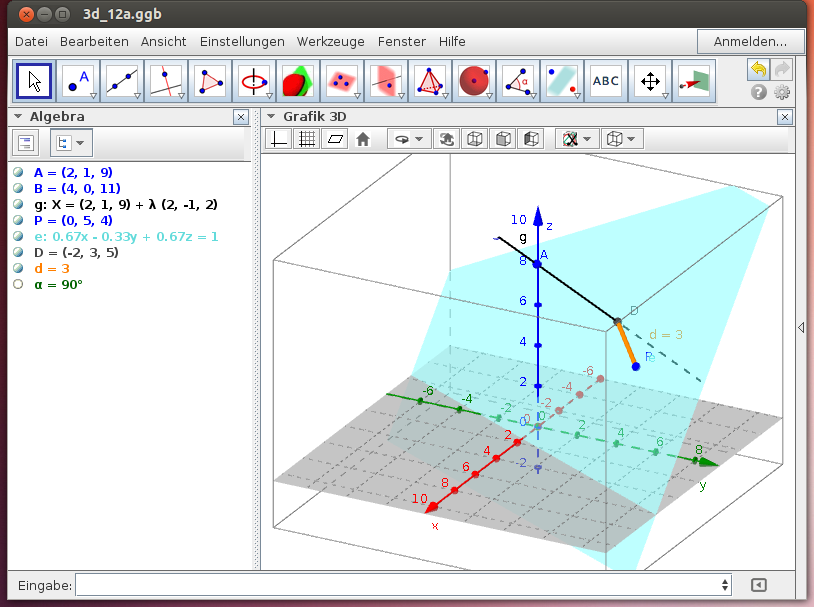
Schneide die Normalebene mit der gegebenen Geraden mit den GeoGebra-Befehl Schneide(<Objekt1>,<Objekt2>) und wähle die Strecke PD mit dem GeoGebra-Befehl Strecke(<Punkt1>,<Punkt2>):
Ergebnis: d = 3
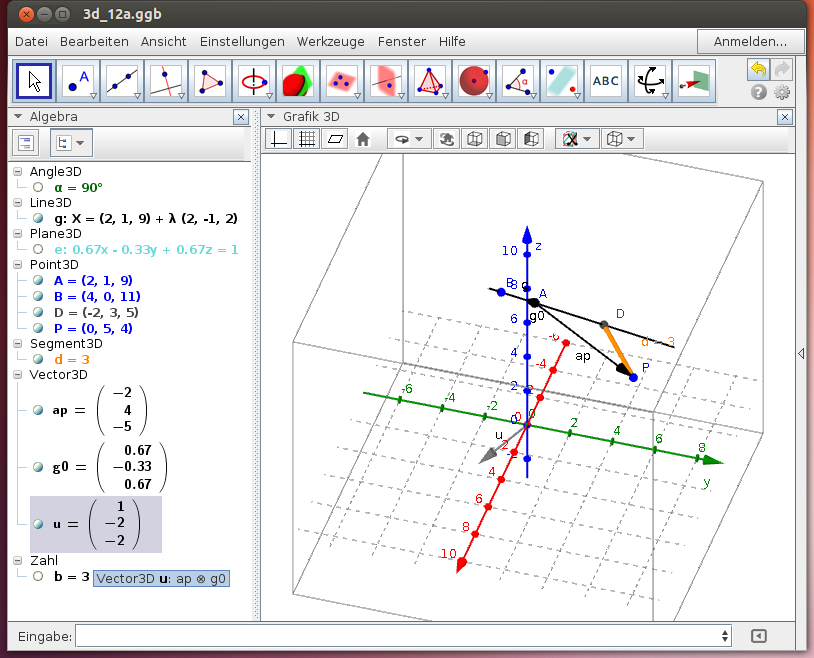
Der Winkel α zwischen der Strecke d und der Geraden g ist ein rechter Winkel …