Volumen eines Körpers mit quadratischen Querschnittsflächen
Von einem Körper ist seine „Seitenansicht“ in der xz-Ebene gegeben; und zwar ist dessen Umriss durch zwei Kurven z1(x) und z2(x), sowie durch die Geraden x = 0 und x = 7 festgelegt.
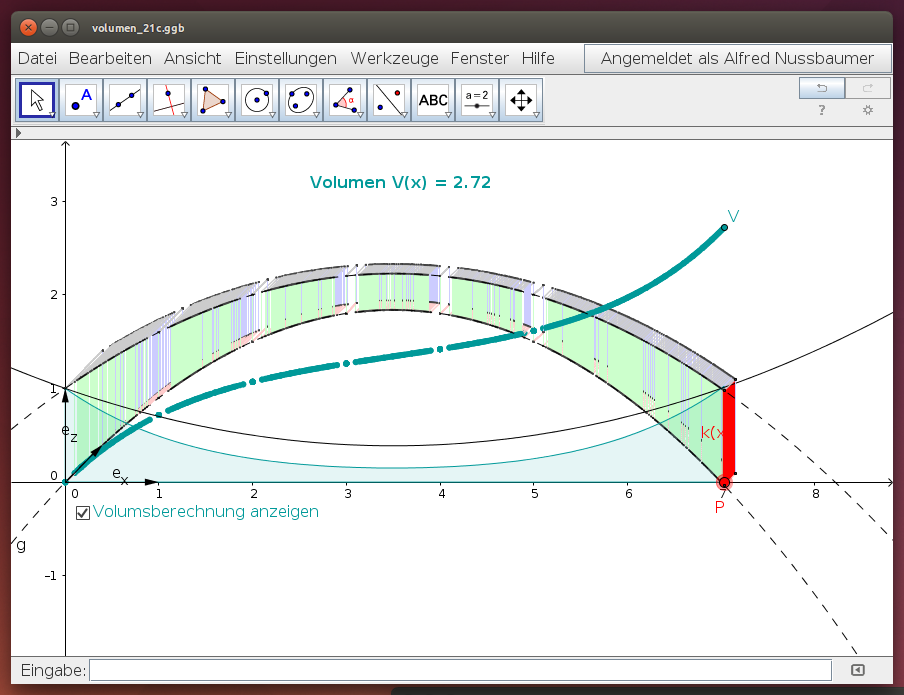
Das Quadrat in der yz-Ebene legt den Körper folgendermaßen fest: Alle Querschnittsflächen stehen normal zur x-Achse; ihre Seitenlänge ist durch die Kante k(x) gegeben.
Verschiebe den roten Punkt P im folgenden GeoGebra-Beispiel und beobachte die Form des Körpers.
Aufgaben:
- Zeige die Volumsberechnung an. Wie lautet das zugehörige bestimmte Integral?
- Die Zunahme des Volumens ist nicht direkt proportional zur Höhe des Körpers - begründe dies!
Zurück zu Anwendungen der Integralrechnung