Inhaltsverzeichnis
Analytische Geometrie
Darstellung von Geraden
Nützliche Befehle:
- Gerade(<Punkt>, <Punkt>) … Erstelle eine Gerade mittels zweier Punkte, eines Punktes und eines Richtungsvektors oder eines Punktes und einer parallelen Geraden
- Parallele … Erstellt eine parallele Gerade (Werkzeug über Icon)
- Senkrechte(g) … Erstellt eine normale Gerade
- Streckensymmetrale(s) … Erstellt eine Streckensymmetrale.
- Winkelsymmetrale(g,h) … Erstellt eine Winkelsymmetrale.
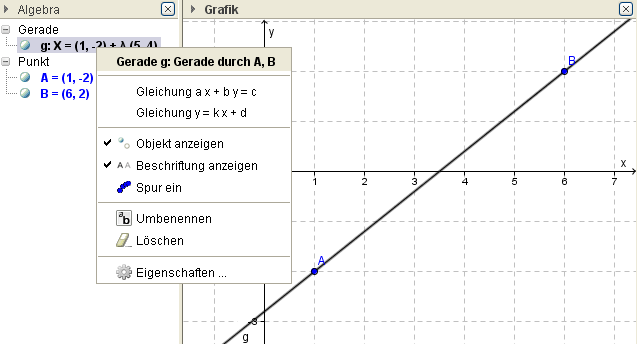
Ex: Stelle die Gerade g[A=(1|-2),B(6|2)] folgenden Formen dar:
a) allgemeine Form, b) explizite Form, c) Parameterform, d) Normalvektorform
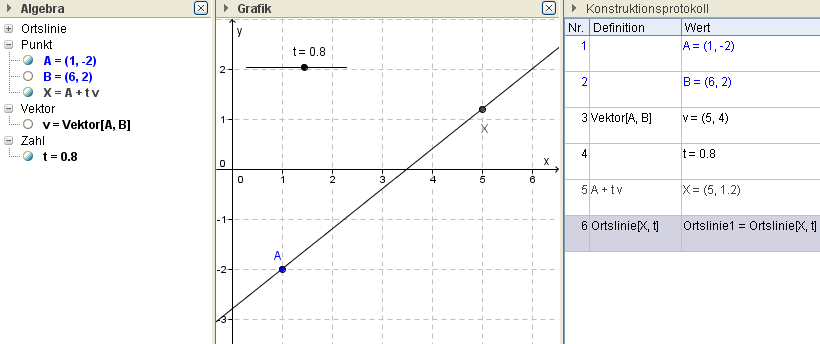
Die Parameterform kann über den Befehl Kurve eingegeben werden.
Schöner ist allerdings die Konstruktion über einen wandernden Punkt.
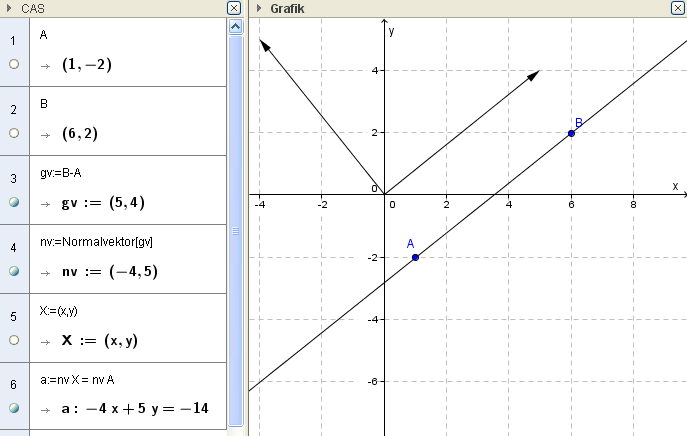
Für die Normalvektorform benötigt man die CAS-Umgebung:
Lagebeziehungen
Abstandsberechnungen
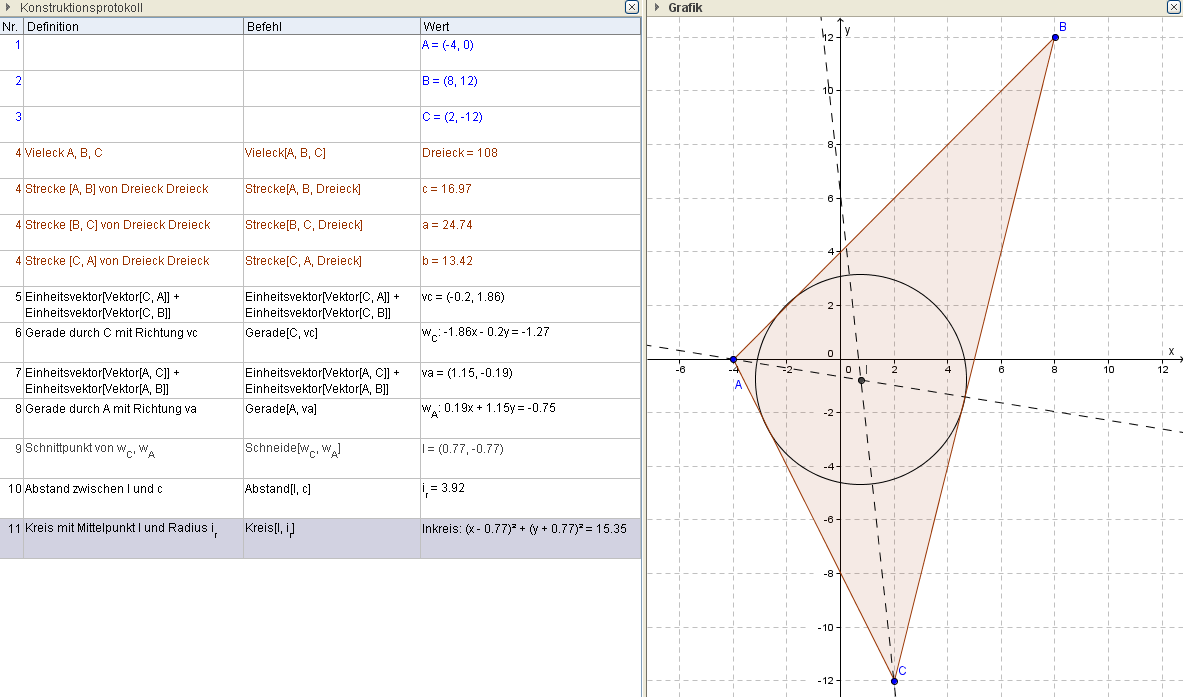
Besondere Punkte im Dreieck
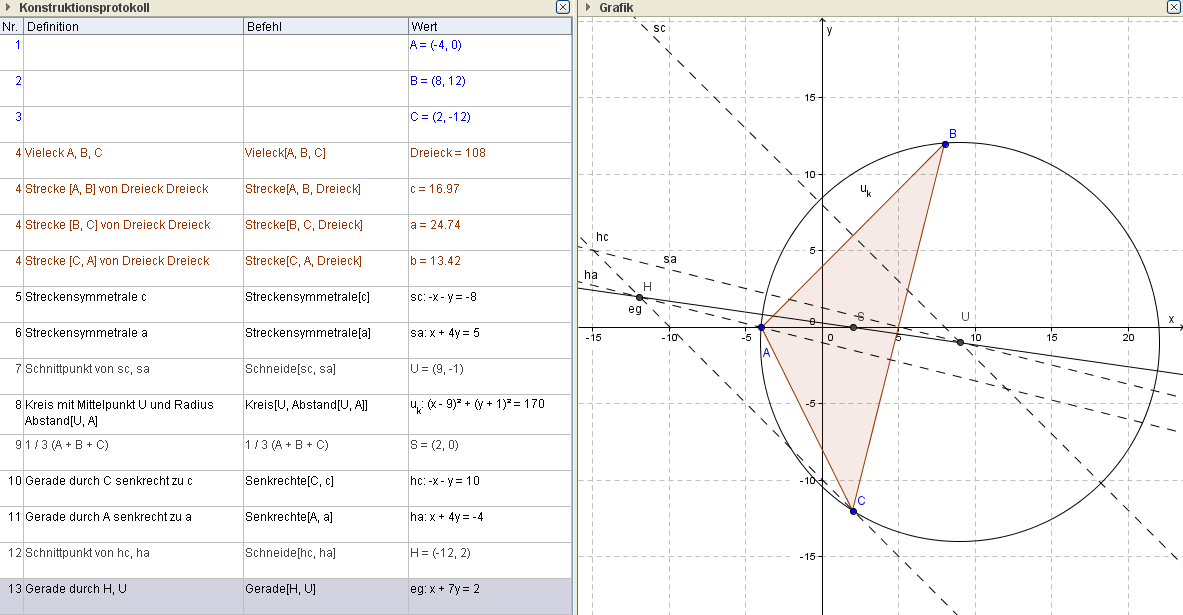
Ex: Berechne für das Dreieck [A=(-4|0),B=(8|12),C=(2|-12)]
a) den Umkreismittelpunkt $U$ und den Umkreis $u_k$,
b) den Höhenschnittpunkt $H$,
c) den Schwerpunkt $S$,
d) den Inkreismittelpunkt $I$ und den Inkreis $i_k$,
e) sowie die Euler'sche Gerade $g_e$.
Beispiele:
- siehe auch: Lehrsätze zum Dreieck
Darstellung von Ebenen
Lagebeziehungen
Ex: Zeige, dass die beiden Ebenen $e_1: x-2y+2z=3$ und $e_2: 2x+y-z=1$ nicht parallel sind und berechne die Gleichung der Schnittgeraden $g$ !