Summenregel für das Differenzieren
Für differenzierbare Funktionen f und g gilt die Ableitungsregel [f + g]' = f' + g'
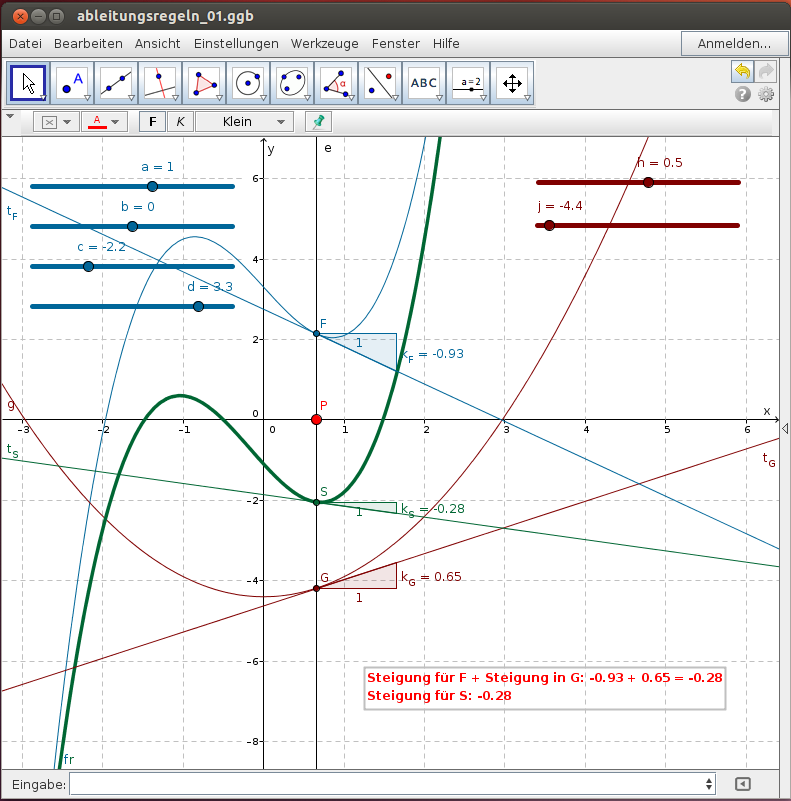
Untersuche für die beiden Funktionen f und g und für ihre Summenfunktion f+g, dass die Summe der Tangentensteigungen für f und g gleich der Tangentensteigung der Summenfunktion f+g für jeden beliebigen Punkt der Kurven ist:
Aufgaben:
- Verschiebe der roten Punkt P auf der x-Achse und überprüfe ob die Steigungen der Tangenten obige Regel erfüllen!
- Wähle die Parameter so, dass die Regel für die Funktionen
und
überprüft wird!
- Skizziere den Beweis für die Summenregel!
Zurück zu Grundlagen der Differentialrechnung | AN2.1