Binomialverteilung: Der Multiple-Choice-Test
Beispiel:
Ein Multiple-Choice-Test besteht aus 24 Aufgaben mit jeweils 6 Antworten, von denen nur jeweils eine richtig ist. Mit welcher Wahrscheinlichkeit kann man durch alleiniges Raten
a) mindestens 4 und höchstens 8 Aufgaben b) mindestens 2 Drittel der Aufgaben richtig beantworten?
Wir rechnen mit dem Wahrscheinlichkeitsrechner:
- n = 24
- p = 1/6
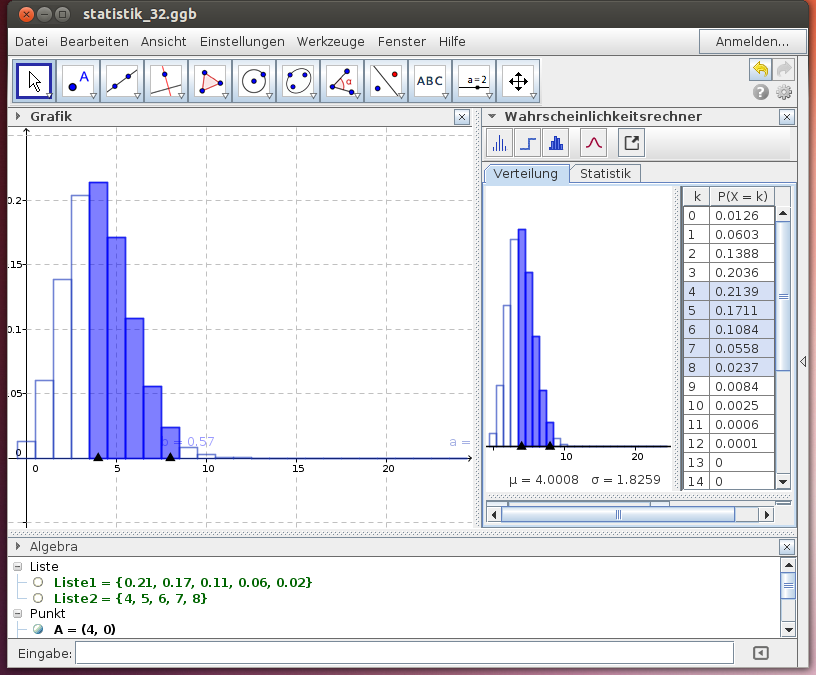
Ergebnis: Mit der Wahrscheinlichkeit 0.2139+0.1711+0.1084+0.0558+0.0237 = 0.5729 ≈ 57,3 % werden zwischen 4 und 8 Aufgaben durch bloßes Raten richtig beantwortet. Mindestens 2/3 aller Aufgaben werden mit der Wahrscheinlichkeit von 0 % durch alleiniges Raten richtig gelöst.
Zurück zu Stochastik | WS3.2