Bewertungsfunktion und Gewinnerwartung: Die Lotterie
Für die diskrete Zufallsvariable X gilt:
Erwartungswert E(g): E(g) = f(0)⋅g(0) + f(1)⋅g(1) + f(2)⋅g(2) + …
Varianz σ²: σ² = V(X) = f(0)⋅(g(0)-E(g))² + f(1)⋅(g(1)-E(g))²⋅1 + f(2)⋅(g(2)-E(g))²⋅2 + …
Standardabweigung σ
(g(x) … Bewertungsfunktion zur diskreten Zufallsvariable X)
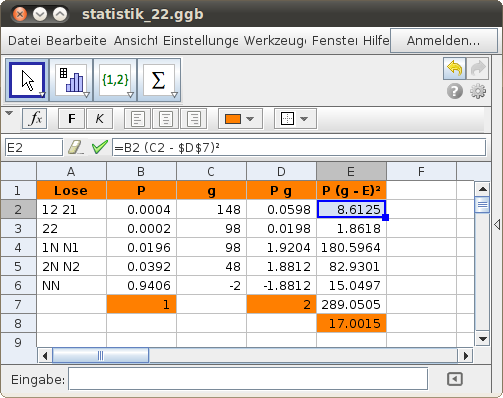
Mit der Tabellenansicht können obige Berechnungen durchgeführt werden.
Beispiel:
Bei einer Lotterie werden 100 Lose zu einem Preis von je 1 GE verkauft: Es gibt ein Los mit dem Hauptgewinn von 100 GE, zwei Lose mit einem Gewinn von je 50 GE. Berechne den zu erwartenden Gewinn und die Standardabweichung, wenn genau zwei Lose gekauft werden!
Ergebnis: μ = 2 GE und σ ≈ 17 GE
Aufgaben:
- Löse ähnliche Aufgaben mit der Tabellenansicht!
Zurück zu Stochastik