Erwartungswert und Varianz: Der Primzahlenwürfel
Für die diskrete Zufallsvariable X gilt:
Erwartungswert μ von X: μ = E(X) = f(0)⋅0 + f(1)⋅1 + f(2)⋅2 + …
Varianz σ² von X: σ² = V(X) = f(0)⋅(0-μ)² + f(1)⋅(1-μ)²⋅1 + f(2)⋅(2-μ)² + …
Standardabweigung σ von X: σ
(f(x) = P(X = x) … Wahrscheinlichkeitsverteilung für die einzelnen Werte von X)
Mit der Tabellenansicht können obige Berechnungen durchgeführt werden.
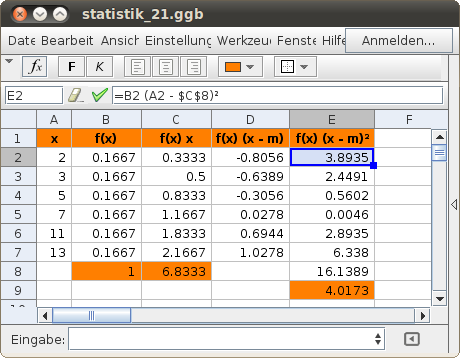
Beispiel:
Der „Primzahlenwürfel“ trägt auf den Seitenflächen die Primzahlen 2, 3, 5, 7, 11 und 13. Berechne den Erwartungswert und die Standardabweichung der Zufallsvariablen X (Augenzahl)!
Ergebnis: μ ≈ 6,8 und σ ≈ 4,0
Aufgaben:
- Löse ähnliche Aufgaben mit der Tabellenansicht!
Zurück zu Stochastik | WS3.1