Partielle Ableitung

7, S. 224 - 225

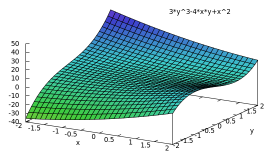
Wir betrachten nun Funktionen in zwei Variablen. Der Graph einer Funktion in zwei Variablen ist im Allgemeinen eine Fläche im Raum:

tex:z = f(x,y)

Solche Flächen lassen sich mit Maxima schnell darstellen (vgl: Maxima: plot3d (Lernpfad)).

Funktionen in zwei unabhängigen Variablen können nach jeder Variablen abgeleitet werden - wir sprechen dann von partiellen Ableitungen:

$tex:\frac {\partial f} {\partial x}$ und $tex:\frac {\partial f} {\partial y}$

Wird noch einmal partiell abgeleitet, sprechen wir von der 2. Ableitung …

Sind die zweiten partiellen Ableitungen stetig, so kann die Reihenfolge der Ableitungen vertauscht werden:

$tex:\frac {\partial^2 f}{\partial x \partial y} = \frac {\partial^2 f}{\partial y \partial x}$

Gegeben ist die Funktion . Bestimme die partiellen Ableitungen!
Überprüfe den Satz von Schwarz!
Rechne nach, ob es im Bereich [-2;2]x[-2;2] ein lokales Extremum gibt!
Untersuche weitere Funktionen mit zwei unabhängigen Variablen: Stelle ihren Graphen als Fläche dar und bestimme partielle Ableitungen und Extrema!

Ableitungen und partielle Ableitungen von Vektoren werden in der Differentialgeometrie verwendet.

Zuletzt angesehen: • partielle_ableitung