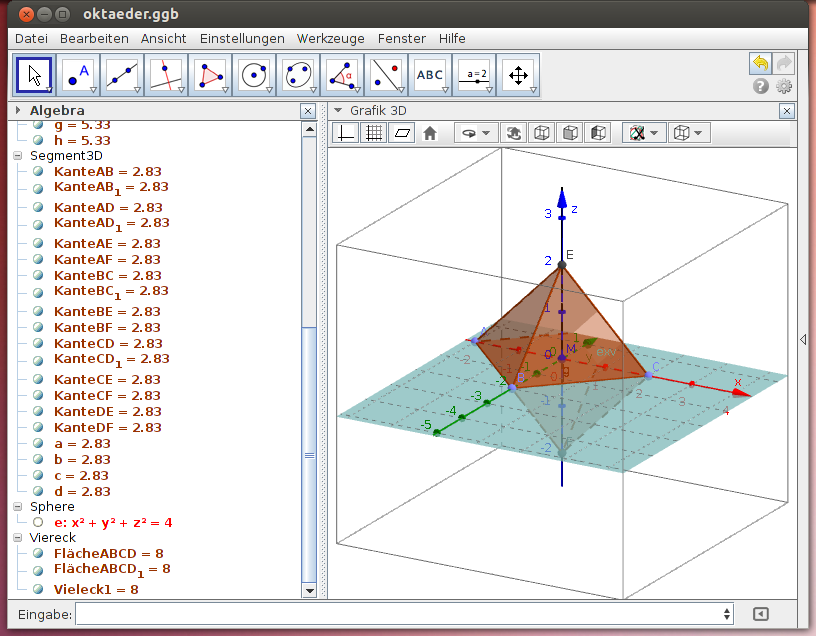
Der Oktaeder
Der Oktaeder besteht aus 8 gleichseitigen Dreiecken. Er kann als „Doppelpyramide“ so konstruiert werden, dass ein Quadrat in einer Kugel, deren Radius der halben Diagonale entspricht, eingeschrieben ist. Dann ergeben sich die Spitzen des Oktaeders als Schnitt der Normalen auf die Quadratebene durch den Mittelpunkt des Quadrats mit der Kugel:
Aufgaben:
- Betrachte den Oktaeder in Richtung zur xy-Ebene, zur xz-Ebene und zur yz-Ebene!
- Überprüfe, dass alle Seitenkanten gleich lang sind!
- Überprüfe, dass alle Seitenflächen gleich groß sind!
- Bestimme die Längen der Raumdiagonalen!
- Konstruiere einen Oktaeder in beliebiger Lage!
- Lies zum Oktaeder nach (WikiPedia:Oktaeder)!
Zurück zu Lernpfad: GeoGebra - GeoGebra 3D | Platonischer Körper