Wo liegen die komplexen Lösungen einer quadratischen Gleichung mit reellen Koeffizienten?
Ein quadratischer Term der Form f(x) = a x² + b y + c legt im Koordinatensystem eine Parabel mit Scheitel S(-b/2a | yS) fest. Dabei sind die Koeffizienten a, b, und c jeweils reelle Zahlen.
Die Nullstellen x1 und x2 dieser Parabel sind die Lösungen der quadratischen Gleichung a x² + b x + c = 0.
Hat die Parabel keine Schnittpunkte mit der x-Achse, so liegen keine reellen Lösungen der zugehörigen quadratischen Gleichung vor.
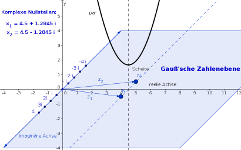
Wo liegen die komplexen Lösungen dieser Gleichung???
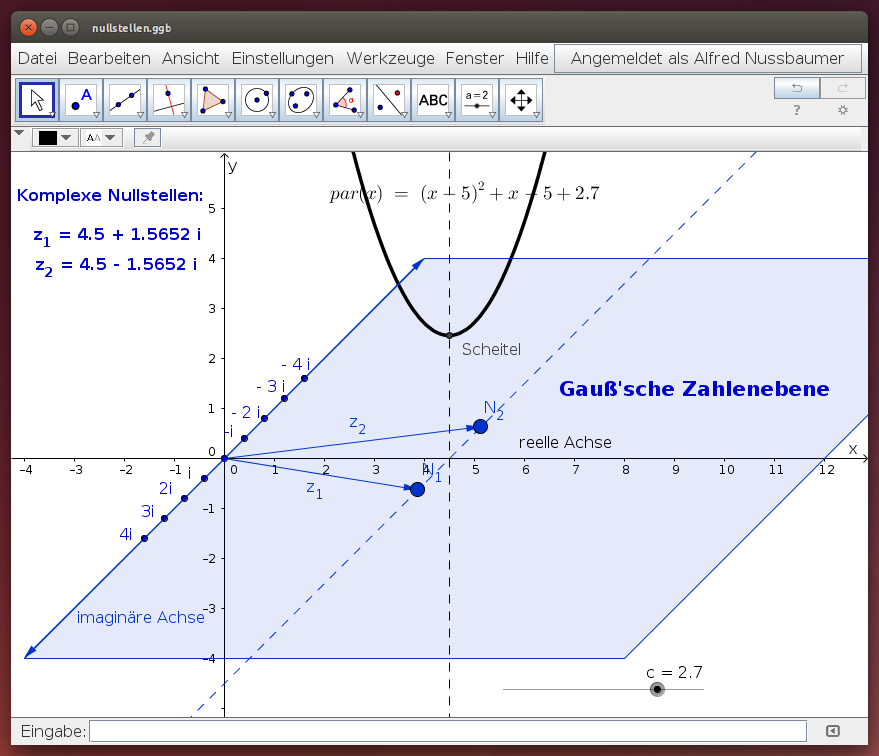
Verschiebe die Parabel im folgenden GeoGebra-Beispiel mit dem Schieberegler für c. Wo liegen die reellen Nullstellen der Parabel und wo liegen die komplexen?
Aufgaben:
- Untersuche die Symmetrien für die reellen Lösungen und formuliere dies für die beiden rellen Nullstellen!
- Welche besonderen Eigenschaften haben die komplexen Lösungen z1 und z2 der quadratischen Gleichung?
Zurück zu Alternative Lösungswege | Komplexe Zahlen und algebraische Gleichungen