Die Standardnormalverteilung
8
Die Normalverteilung (Gauß-Verteilung) ist ein wichtiger Vertreter stetiger Wahrscheinlichkeitsverteilungen. Wir verwenden sie für Beschreibung von zufälligen Vorgängen, wie beispielsweise die zufälligen Abweichungen von der Nennfüllmenge bei Abfüllanlagen oder die zufälligen Abweichungen vom Nennmaß bei der Herstellung von Werkstücken.
Die Standardnormalverteilung ![tex:f(z) = \frac 1 {\sqrt{2 \pi}} \cdot e^{- \frac 1 2 z^2}]()
geht aus der Normalverteilung ![tex:f(x) = \frac 1 {\sigma \cdot \sqrt{2 \pi}} \cdot e^{- \frac 1 2 \cdot \left ( \frac {x - \mu} \sigma \right)^2}]()
durch die Transformation ![tex:z = \frac {x - \mu} \sigma]()
hervor.
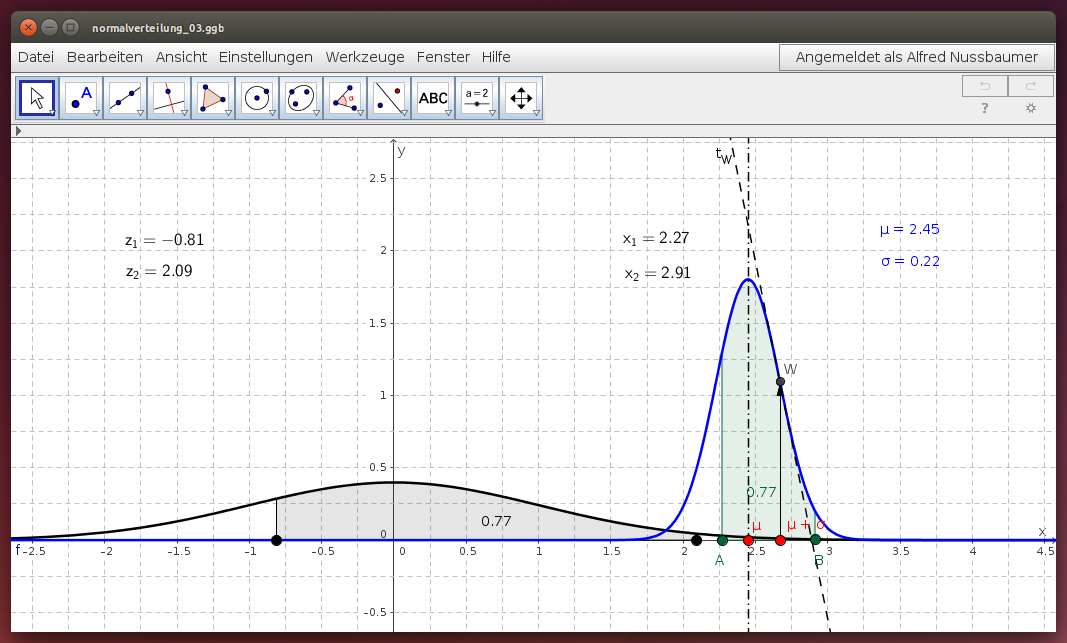
Untersuche die Eigenschaften der Standardnormalverteilung mit dem folgenden GeoGebra-Modell:
Aufgaben:
- Untersuche, wie sich die Form der Standardnormalverteilung ändert, wenn du verschiedene Werte für μ und σ der Normalverteilung wählst!
- Überprüfe, dass der Erwartungswert der Standardnormalverteilung 0 ist!
- Überprüfe, dass die Standardabweichung der Standardnormalverteilung 1 ist!
- Wähle verschiedene Intervallgrenzen mit Hilfe der Punkte A und B und überprüfe die Werte der Integrale unter der Normalverteilung und unter der Standardnormalverteilung!
- Rechne die im GeoGebra-Applet angezeigten Werte für die Intervallgrenzen der Standardnormalverteilung z1 und z2 aus den Intervallgrenzen x1 und x2 der Normalverteilung nach!
Zurück zu Stochastik
