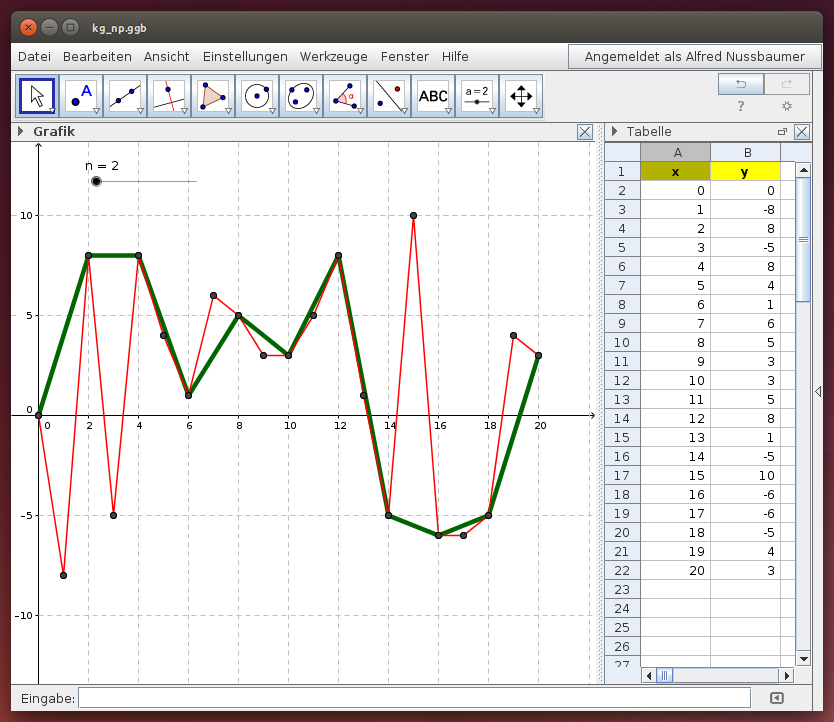
Kurvenglättung: Der n-Punkt-Algorithmus
Beim n-Punkt-Algorithmus wird aus einer Folge von gegebenen Punkten ausgehend vom Anfangspunkt jeder n-te Punkt ausgewählt. Die dazwischen liegenden Punkte werden verworfen.
Untersuche dies für die im folgenden GeoGebra-Beispiel gegebene Kurve mit zufälligen Ordinatenwerten zwischen -10 und 10 für verschiedene Werte für n:
Aufgaben:
- Wähle verschiedene Werte für n und beschreibe die Güte der Näherung!
- Untersuche, bei welcher Ausgangskurve der n-Punkt-Algorithmus zur Kurvenglättung geeignet, und bei welcher Ausgangskurve der n-Punkt-Algorithmus wenig geeignet ist!
- Beschreibe die Schwachstelle des n-Punkt-Algorithmus!
Hinweis: Mit <strg>-R werden alle Objekte neu berechnet; die Ordinaten der 20 Kurvenpunkte erhalten neue Zufallswerte zwischen -10 und 10.
Ausblick:
Die Güte der Näherung kann untersucht werden, indem die Normalabstände der verworfenen Punkte zum Streckenzug berechnet und addiert werden. Gib ein Verfahren dazu an!
Zurück zu Kurvenglättung | Analytische Geometrie der Ebene