Das Räuber-Beute-Modell
(zu 
8, S. 148)
Dynamische Systeme mit mehreren Bestandsgrößen treten in den Natur häufig auf. In Räuber-Beute-Modellen werden die Abhängigkeiten zwischen Beutetieren und Räubern in einem Gleichungssystem dargestellt, in dem das Wachstumsrate (Zunahme der Population pro Zeitschritt) und die Sterberate (Abnahme der Population pro Zeitschritt) für zwei Bestandsgrößen dargestellt wird:
Für die Beutetiere x gilt:
(Anzahl der Beutetiere nach einem Zeitschritt)
Dabei beschreibt wb das Wachstum der Beutetiere und tb die Abnahme durch das Gefressenwerden durch die Räuber.
Für die Räuber y gilt:
(Anzahl der Räuber nach einem Zeitschritt)
tr beschreibt dabei die natürliche Sterberate der Räuber und wr die Reproduktion (u.A. auf der Basis der zur Verfügung stehenden Nahrung durch die vorhandenen Beutetiere).
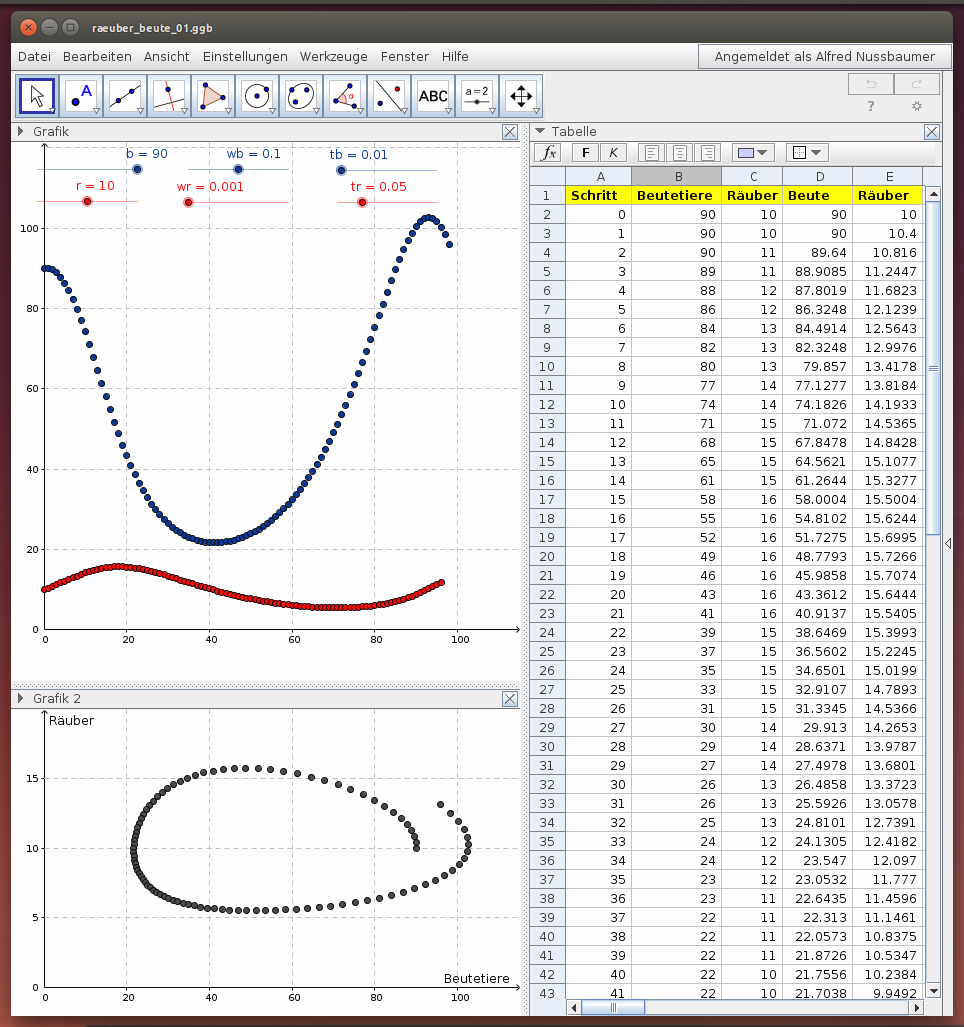
Die beiden Differenzengleichungen erlauben das schrittweise Berechnen der jeweiligen Individuenzahl in zwei Spalten. In der ersten Grafik wird die zeitliche Entwicklung der Beutetiere und der Räuber dargestellt (Zeitdiagramm). Die zweite Grafik zeigt, wie die beiden Populationen voneinander abhängen (Phasendiagramm):
Aufgaben
Beutetiere b und die Anzahl der Räuber r zum Zeitpunkt 0 und interpretiere die Entwicklung beider Populationen!
- Variiere die einzelnen Parameter tb, wb, tr und tw und interpretiere die Auswirkungen!
- Recherchiere zum Räuber-Beute-Modell!
- Vergleiche
6, Thema Biomathematik!
- Vergleiche 6, Füchse und Hasen!
- Löse weitere Aufgabenstellungen - analog zu den Aufgaben 561, 591, 592, 593 und 594!
- Stelle symbiotische und konkurrenzierende Systeme in geeigneten Modellen dar und untersuche ihr Verhalten (vgl. 8 S. 149)!
Ausblick
Untersuche das Langzeitverhalten von Systemen anhand bekannter Simulationen:
- Wator
- Game of Life
- Zelluläre Automaten
Hinweis: Gute Ausgangspunkte für die obigen Modelle sind im Onlinelexikon WikiPedia nachzulesen.
