Das Prinzip von Cavalieri
(zu 
8, S. 72 - 73)
Bonaventura Francesco Cavalieri (1598 - 1657) war ein italienischer Mönch, Mathematiker und Astronom. Mit seinen Berechnungen von Oberflächen und Rauminhalten nahm er Methoden der Differential- und Integralrechnung vorweg.
In der Schulmathematik verwenden wir das Cavalierische Prinzip:
Dieses Prinzip lässt sich mit verschiedenen, gleich hohen Stößen gleicher Geldmünzen leicht veranschaulichen:
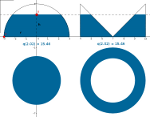
Wir verwenden das Prinzip von Cavalieri hier, um die Formel für das Volumen einer Halbkugel (und somit für die Kugel) nach Archimedes zu zeigen: Das Volumen der Halbkugel entspricht dem Volumen eines Drehzylinders mit gleichem Radius und Höhe, aus dem ein Kreiskegel mit gleichem Radius und Höhe herausgeschnitten wird …
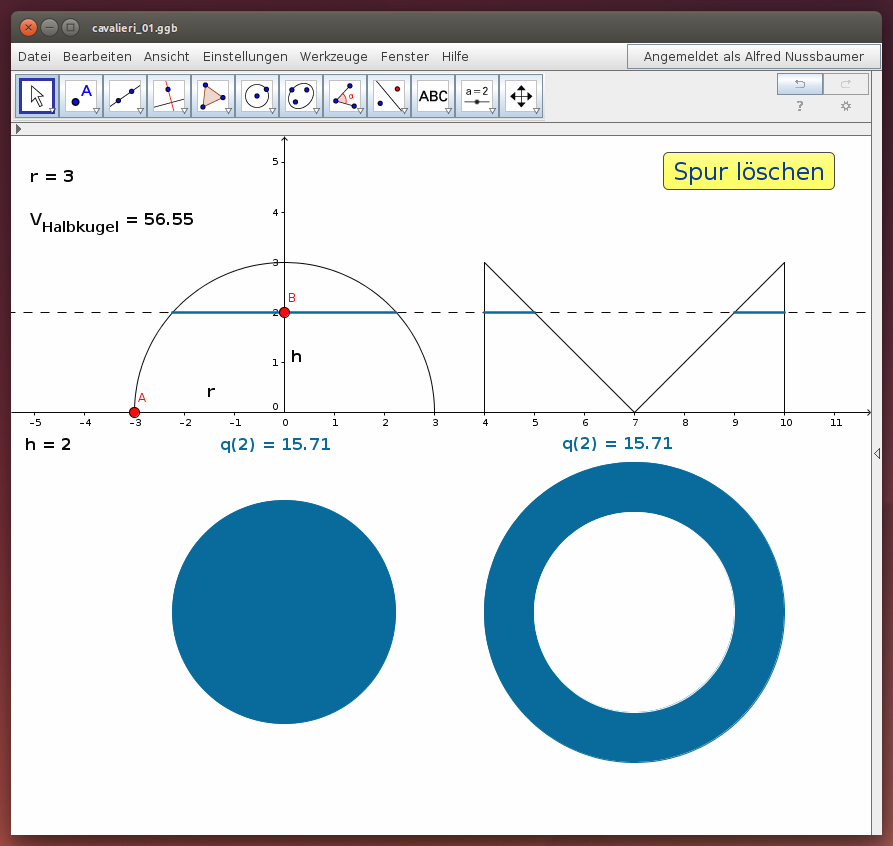
Verschiebe im folgenden GeoGebra-Applet den roten Punkt B entlang der Kugelachse, um die Flächeninhalte der zugehörigen Schnittflächen zu vergleichen:
(Hinweis: Lösche die Spur der Strecken mit der Schaltfläche „Spur löschen“.)
Aufgaben
Die Schnitthöhe h wird durch die Position des Punktes B bestimmt.
- Gib eine Formel für den Flächeninhalt des Schnittkreises der Halbkugel in Abhängigkeit von der Schnitthöhe h an!
- Gib eine Formel für den Flächeninhalt des Kreisringes in Abhängigkeit von der Schnitthöhe h an!
- Überprüfe, dass die beiden Flächeninhalte gleich sind (vergleiche
8, S. 73)!
