Umkehraufgabe (Polynomfunktion 4. Grades)
Von einer Polynomfunktion 4. Grades sind zwei Punkte und ein Wendepunkt mit Wendetangente gegeben. Bestimme den Funktionsterm!
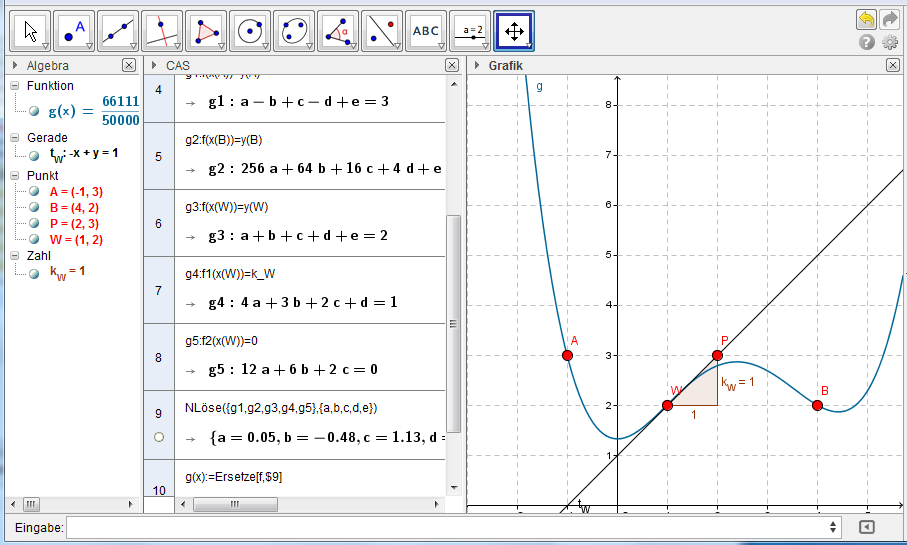
Arbeiten mit dem CAS:
- Definiere die Polynomfunktion 4. Grades allgemein (
f(x) = a x^4 + b x^3 + c x^2 + d x + e)! - Definiere die erste und zweite Ableitung der Funktion (
f1(x) = f'(x),f2(x) = f1'(x))! - Definiere alle Gleichungen in der CAS-Ansicht (z.B.:
g1:f(x(A) = y(A)oderg5:f2(x(W))=0); - Löse das auftretende lineare Gleichungssystem!
- Ersetze die Platzhalter
,
,
,
und
durch die ermittelten Lösungen (
g(x):=Ersetze(f,$9), dabei enthält die Zeile 9 in der CAS-Ansicht die Liste der Lösungen für,
,
,
und
).
- Stelle die Funktion tex:f(x) grafisch dar und überprüfe die Übereinstimmung mit den gegebenen Punkten!
Zurück zu Eigenschaften von Funktionen